Lcm Of 15 And 2
seoindie
Sep 16, 2025 · 6 min read
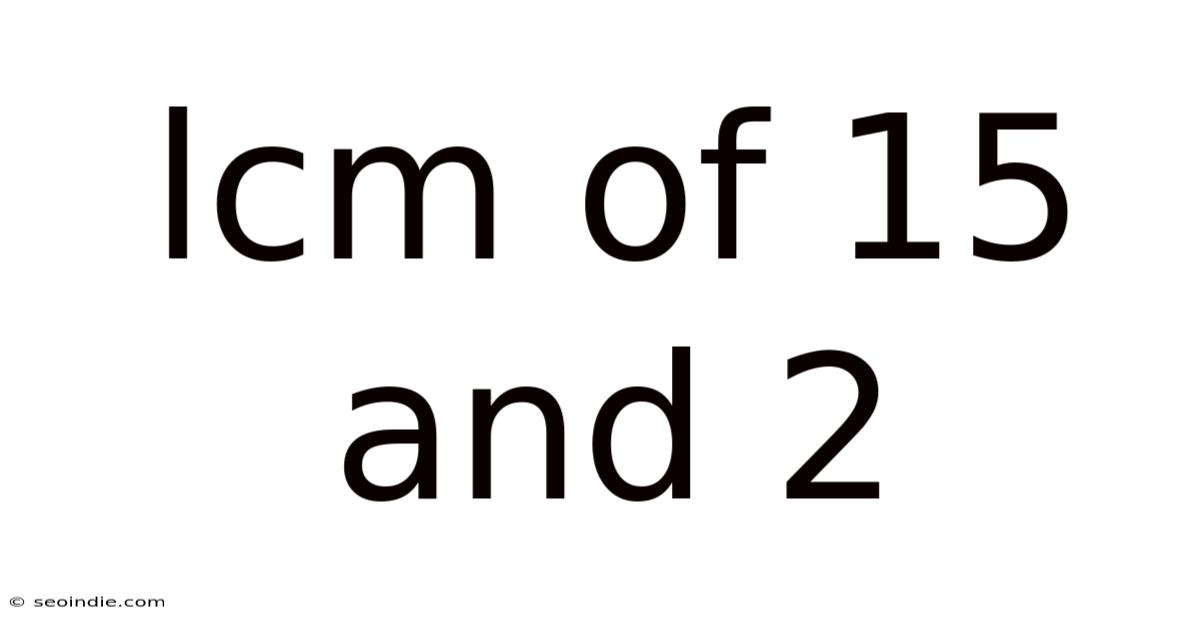
Table of Contents
Understanding the Least Common Multiple (LCM) of 15 and 2: A Deep Dive
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 15 and 2. However, grasping the underlying concepts and exploring different methods for calculating the LCM provides a solid foundation for understanding more complex mathematical concepts later on. This article will delve into the LCM of 15 and 2, explaining the process step-by-step, exploring different calculation methods, and offering insights into its applications. We’ll also touch upon the connection between LCM and the Greatest Common Divisor (GCD), solidifying your understanding of these fundamental number theory concepts.
Introduction to Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding the LCM is crucial in various mathematical operations, particularly when working with fractions, simplifying expressions, and solving problems related to cycles and patterns. This article will focus on finding the LCM of 15 and 2, but the methods discussed can be applied to find the LCM of any two integers.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32...
By comparing the lists, we can see that the smallest number that appears in both lists is 30. Therefore, the LCM of 15 and 2 is 30. This method is simple for smaller numbers but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
Prime factorization is a more powerful and efficient method for finding the LCM, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors.
- Prime factorization of 15: 3 x 5
- Prime factorization of 2: 2
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations of the given numbers.
- The prime factors involved are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together gives us the LCM: 2 x 3 x 5 = 30. This method is more systematic and efficient, especially for larger numbers where listing multiples becomes impractical.
Method 3: Using the Formula (LCM and GCD Relationship)
There's a direct relationship between the Least Common Multiple (LCM) and the Greatest Common Divisor (GCD) of two numbers. The formula is:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 15 and 2. The GCD is the largest number that divides both 15 and 2 without leaving a remainder. In this case, the GCD(15, 2) = 1 because 1 is the only common divisor of 15 and 2.
Now, using the formula:
LCM(15, 2) * GCD(15, 2) = 15 * 2 LCM(15, 2) * 1 = 30 LCM(15, 2) = 30
This method highlights the interconnectedness of LCM and GCD, offering a more sophisticated approach to solving the problem. It is particularly useful when dealing with larger numbers where finding the GCD using the Euclidean algorithm is more efficient than directly finding the LCM through other methods.
Understanding the Concept of Divisibility
The LCM of 15 and 2 being 30 implies that 30 is divisible by both 15 and 2. Divisibility means that when you divide 30 by 15 or 2, the remainder is zero. This is a fundamental concept in number theory and is used extensively in various applications. Understanding divisibility helps in simplifying fractions, finding common denominators, and solving various mathematical problems.
Applications of LCM
The concept of LCM has practical applications in various fields:
-
Scheduling: Imagine two buses arriving at a bus stop at different intervals. One bus arrives every 15 minutes, and the other every 2 minutes. The LCM (15, 2) = 30 indicates that both buses will arrive at the bus stop simultaneously every 30 minutes.
-
Fraction Operations: When adding or subtracting fractions, you need a common denominator, which is the LCM of the denominators. For example, adding 1/15 and 1/2 requires finding the LCM of 15 and 2 (which is 30) to obtain a common denominator.
-
Cyclic Patterns: LCM is used to determine when events with different cyclical patterns will coincide. This is applicable in various fields, including astronomy, engineering, and computer science.
Further Exploration: Euclidean Algorithm and Larger Numbers
While the methods described above are sufficient for finding the LCM of 15 and 2, for larger numbers, the Euclidean algorithm is a more efficient method for finding the GCD, which, as shown earlier, can then be used to calculate the LCM. The Euclidean algorithm is a systematic approach to finding the GCD of two numbers through successive divisions.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of both given numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both given numbers without leaving a remainder.
Q2: Can the LCM of two numbers be equal to one of the numbers?
A2: Yes, if one number is a multiple of the other. For example, the LCM of 6 and 3 is 6.
Q3: Is there a limit to how large the LCM can be?
A3: No, the LCM can be arbitrarily large depending on the size of the given numbers.
Q4: How can I find the LCM of more than two numbers?
A4: You can extend the prime factorization method. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM.
Conclusion
Finding the LCM of 15 and 2, while seemingly simple, provides a valuable opportunity to understand fundamental mathematical concepts like divisibility, prime factorization, and the relationship between LCM and GCD. The methods discussed – listing multiples, prime factorization, and using the LCM-GCD formula – offer different approaches to solving the problem, each with its own strengths and weaknesses. Mastering these methods builds a solid foundation for tackling more complex mathematical challenges involving larger numbers and more intricate problems. Understanding LCM is not just about performing calculations; it's about appreciating the underlying mathematical principles and their broad applications in various fields. The ability to efficiently calculate the LCM is a key skill in many areas of mathematics and beyond.
Latest Posts
Latest Posts
-
Hardest Tissue Of The Body
Sep 16, 2025
-
3 Meters How Many Inches
Sep 16, 2025
-
What Are Measures Of Dispersion
Sep 16, 2025
-
Is 3 0 A Whole Number
Sep 16, 2025
-
Factors Of 125 In Pairs
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.