Is 3.0 A Whole Number
seoindie
Sep 16, 2025 · 6 min read
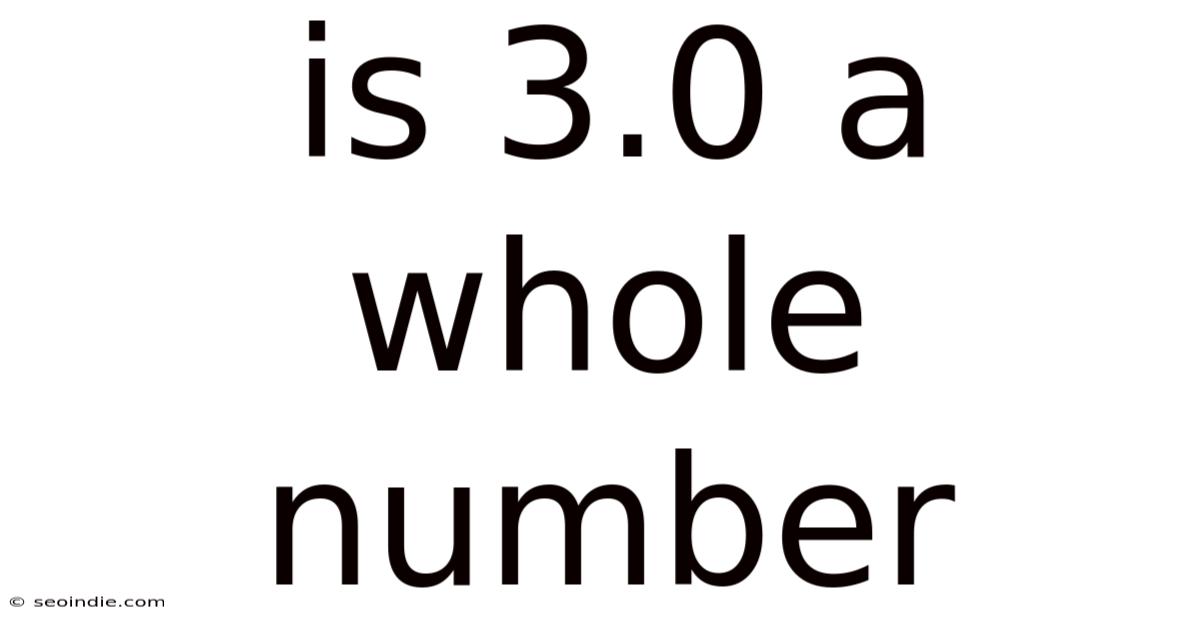
Table of Contents
Is 3.0 a Whole Number? A Deep Dive into Number Systems
Is 3.0 a whole number? The seemingly simple question belies a deeper understanding of number systems and mathematical classifications. At first glance, the answer might seem obvious, but a closer examination reveals nuances that are crucial for a solid grasp of mathematical concepts. This article will explore the definition of whole numbers, decimal numbers, and the relationship between them, ultimately clarifying the status of 3.0 within these classifications. We'll delve into the practical implications of this understanding and answer frequently asked questions about related concepts.
Understanding Whole Numbers
The foundation of our exploration lies in the precise definition of whole numbers. Whole numbers are the set of non-negative integers, starting from zero and extending infinitely. This set can be represented as {0, 1, 2, 3, 4, 5, ...}. Crucially, whole numbers do not include fractions, decimals, or negative numbers. They represent complete, undivided units. Think of counting discrete objects: apples, cars, or people. You can have three apples, but you can't have three and a half apples in the context of whole numbers.
Decimals and Their Representation
Decimal numbers, on the other hand, are numbers that contain a decimal point, separating the whole number part from the fractional part. The number 3.0 is a decimal number. The ".0" signifies that there is no fractional part; the value is exactly three. This representation is often used to emphasize precision or to differentiate it from a number like 3, which might be considered an integer in some contexts. Decimals can represent both whole numbers (like 3.0, 10.0, 100.0) and numbers with fractional parts (like 3.14, 2.5, 0.75).
The Relationship Between Whole Numbers and Decimals
The key relationship to understand is that whole numbers are a subset of decimal numbers. Any whole number can be represented as a decimal number by simply adding ".0" to the end. For example, the whole number 3 can be written as the decimal 3.0. However, the reverse isn't always true. Not all decimal numbers are whole numbers. Decimals like 3.14 or 2.718 are not whole numbers because they possess a non-zero fractional component.
Why the Distinction Matters
Understanding the difference between whole numbers and decimal numbers is critical in various mathematical and real-world applications.
-
Computer Science: Many programming languages have specific data types for integers and floating-point numbers (which include decimals). Choosing the correct data type is crucial for efficient memory management and accurate calculations. Using a whole number data type for 3 is more efficient than using a floating-point type for 3.0, but that efficiency comes with limitations. Using the incorrect data type may lead to errors.
-
Measurement: In scientific measurements, decimals are frequently used to express precision. For example, measuring the length of an object may yield 3.0 centimeters, indicating greater accuracy than a measurement of 3 centimeters. The ".0" suggests that the measurement was made with sufficient precision to confirm that there is no fractional part.
-
Finance: Accounting and financial applications often require high precision. While a whole number might suffice for counting items, financial transactions usually demand decimal representation to represent cents or fractions of a currency unit.
-
Statistical Analysis: Statistical calculations may involve both whole numbers and decimal numbers. The use of decimals allows for a more nuanced understanding of statistical data and permits for a wider range of calculations.
-
Mathematical Operations: Different mathematical operations can affect the outcome. Adding a whole number and a decimal may result in a decimal (e.g., 3 + 2.5 = 5.5), while adding two whole numbers will always result in a whole number (e.g., 3 + 2 = 5).
The Case of 3.0: A Whole Number in Decimal Clothing
Given the definitions and relationships discussed, we can confidently answer the initial question: Yes, 3.0 is a whole number. It satisfies the criteria of being a non-negative integer. The ".0" simply represents it in decimal form, a more precise way of denoting its value, particularly within contexts where decimal representation is necessary for accuracy or consistency. It's essentially a whole number expressed using decimal notation. It's analogous to saying that "one dollar" is the same as "one hundred cents"; the representation differs, but the underlying value is identical.
Beyond the Basics: Different Number Systems
Our discussion so far has focused on the decimal system (base-10), which is the most common number system. However, other number systems exist, such as binary (base-2) used in computers, or hexadecimal (base-16) used in color codes. The concept of whole numbers remains consistent across these systems. For example, the binary representation of 3 is 11, and the hexadecimal representation is 3. Despite the different notations, the underlying value remains the same and still fits the definition of a whole number.
Expanding the Number Line: Integers and Beyond
It’s important to situate whole numbers within the broader context of the number line. Whole numbers are a subset of integers. Integers include all whole numbers and their negative counterparts: {... -3, -2, -1, 0, 1, 2, 3 ...}. Beyond integers, we have rational numbers (numbers that can be expressed as a fraction of two integers), irrational numbers (numbers that cannot be expressed as a fraction, such as π), and real numbers (which encompass all rational and irrational numbers). Understanding these relationships provides a complete picture of the mathematical landscape.
Frequently Asked Questions (FAQ)
-
Q: Is 3.000 the same as 3.0? A: Yes, both represent the same value; the additional zeros after the decimal point simply increase precision without altering the underlying value.
-
Q: Can a whole number be negative? A: No. By definition, whole numbers are non-negative. Negative numbers are included in the set of integers.
-
Q: Is 0 a whole number? A: Yes, 0 is the first whole number.
-
Q: What is the difference between an integer and a whole number? A: Whole numbers are non-negative integers (0, 1, 2, 3...). Integers include all whole numbers and their negative counterparts (...-3, -2, -1, 0, 1, 2, 3...).
-
Q: If 3.0 is a whole number, why do we use the decimal point? A: The decimal point is used to maintain consistency in mathematical operations and data representation, especially in contexts that also utilize numbers with fractional parts. It ensures clarity and prevents ambiguity.
Conclusion
The question of whether 3.0 is a whole number is not simply a matter of semantics; it highlights the crucial distinctions between different number systems and their classifications. While 3.0 is represented as a decimal number, its value aligns precisely with the definition of a whole number: a non-negative integer. The decimal point signifies precision and consistency in numerical representation, particularly within the context of broader mathematical operations and applications. Understanding these distinctions is fundamental for grasping more complex mathematical concepts and applying them effectively in diverse fields. The seemingly simple number 3.0 serves as a powerful gateway to a deeper appreciation of the intricacies and elegance of mathematics.
Latest Posts
Latest Posts
-
Differentiate Between Pollination And Fertilization
Sep 16, 2025
-
Soda Ash In A Pool
Sep 16, 2025
-
What Numbers Go Into 21
Sep 16, 2025
-
Words To Describe My Daughter
Sep 16, 2025
-
Maharashtra State Board History Textbook
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 3.0 A Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.