Factors Of 125 In Pairs
seoindie
Sep 16, 2025 · 6 min read
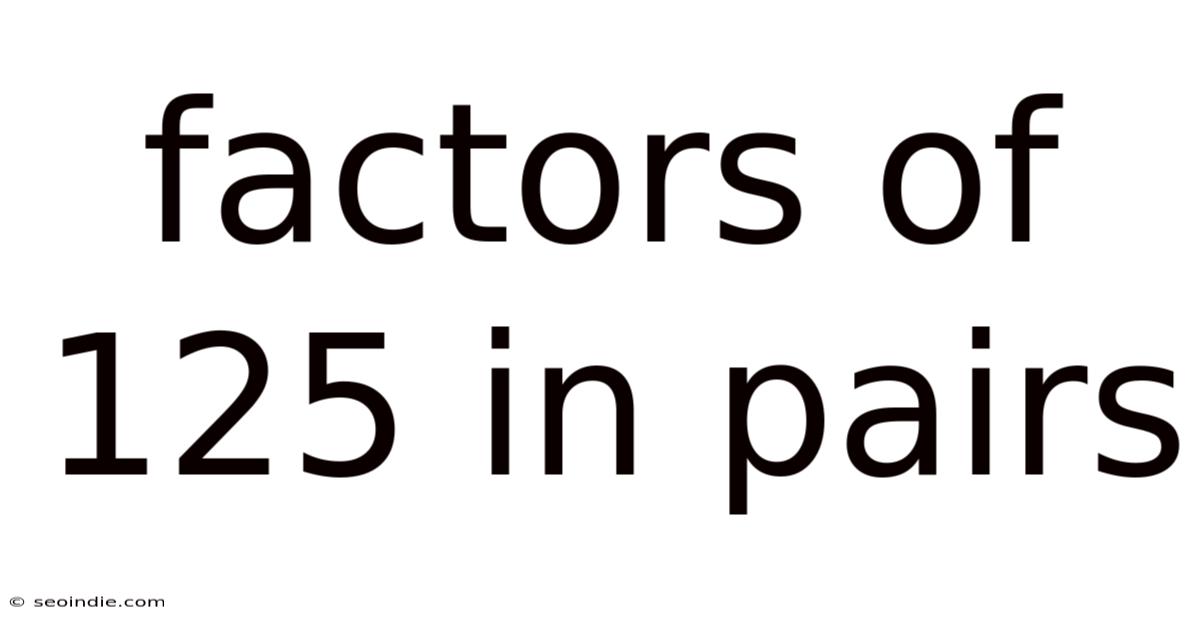
Table of Contents
Unveiling the Factors of 125: A Deep Dive into Pairs and Beyond
Finding the factors of a number might seem like a simple arithmetic task, but delving deeper reveals a fascinating world of number theory. This article explores the factors of 125, focusing on how they pair up and the underlying mathematical principles governing their relationships. Understanding factors is crucial for various mathematical concepts, including prime factorization, greatest common divisors (GCD), and least common multiples (LCM). We will not only identify the factor pairs of 125 but also explore the broader context of factorization and its applications.
Understanding Factors
A factor of a number is a whole number that divides the number evenly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Finding all the factors of a number is a fundamental skill in arithmetic and algebra.
Finding the Factors of 125
To find the factors of 125, we systematically look for whole numbers that divide 125 without leaving a remainder. We can start by checking the smallest whole numbers:
- 1: 125 divided by 1 is 125, so 1 is a factor.
- 5: 125 divided by 5 is 25, so 5 is a factor.
- 25: 125 divided by 25 is 5, so 25 is a factor.
- 125: 125 divided by 125 is 1, so 125 is a factor.
Therefore, the factors of 125 are 1, 5, 25, and 125.
Factor Pairs of 125
Factors often come in pairs. When we multiply two factors together, we get the original number. Let's identify the factor pairs of 125:
- 1 x 125 = 125 This is the first factor pair.
- 5 x 25 = 125 This is the second factor pair.
Notice that the number 125 is an odd number. Odd numbers generally have an odd number of factors. In the case of 125, the factors are 1, 5, 25, and 125, which totals four factors, as expected. These factors are paired as mentioned above.
Prime Factorization of 125
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
The prime factorization of 125 is 5 x 5 x 5, or 5³. This means that 125 is a perfect cube, meaning it is the cube of a whole number (5³ = 125). This prime factorization helps us understand the structure of the number and is fundamental in various mathematical applications. The prime factorization directly informs us about all the possible factors of 125. Any combination of the prime factors (5s in this case) will also be a factor.
For example:
- 5⁰ = 1 (a factor)
- 5¹ = 5 (a factor)
- 5² = 25 (a factor)
- 5³ = 125 (a factor)
The Significance of Factor Pairs
Understanding factor pairs is important for several reasons:
-
Simplifying Fractions: When simplifying fractions, finding the greatest common factor (GCF) of the numerator and denominator is crucial. The GCF is the largest number that divides both the numerator and denominator evenly. Factor pairs help identify the GCF.
-
Solving Algebraic Equations: Factor pairs are essential in factoring quadratic equations and other polynomial expressions. Factoring allows us to simplify equations and solve for unknown variables.
-
Number Theory: Factor pairs and prime factorization are fundamental concepts in number theory, a branch of mathematics that explores the properties of numbers.
-
Cryptography: Prime factorization plays a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. The difficulty of factoring large numbers into their prime factors forms the basis of the security of these systems.
Exploring Factors Beyond Pairs: Divisibility Rules
While we've focused on factor pairs, it's helpful to understand divisibility rules, which provide shortcuts to determine if a number is divisible by another. Knowing these rules can speed up the process of identifying factors.
- Divisibility by 1: Every number is divisible by 1.
- Divisibility by 5: A number is divisible by 5 if its last digit is either 0 or 5. This rule directly applies to 125 because it ends in 5.
- Divisibility by 25: A number is divisible by 25 if its last two digits are divisible by 25. Since 25 is divisible by 25, 125 is divisible by 25.
Further Exploration: Factors of Other Numbers
Let's briefly compare the factors of 125 to other numbers to illustrate the diversity of factorization:
-
Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100. 100 has more factors than 125 and exhibits different factor pairs. Its prime factorization is 2² x 5².
-
Factors of 10: 1, 2, 5, 10. A smaller number with fewer factors and different factor pairs. Its prime factorization is 2 x 5.
-
Factors of 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144. A larger number with many factors showcasing diverse pairs and revealing a prime factorization of 2⁴ x 3².
These examples highlight how the number of factors and their arrangement vary significantly depending on the number's prime factorization and structure.
Frequently Asked Questions (FAQ)
Q: What is the greatest common factor (GCF) of 125 and 25?
A: The GCF of 125 and 25 is 25, as 25 is the largest number that divides both 125 and 25 evenly.
Q: What is the least common multiple (LCM) of 125 and 25?
A: The LCM of 125 and 25 is 125, since 125 is a multiple of 25.
Q: Can a number have an infinite number of factors?
A: No, a whole number can only have a finite number of factors.
Q: How can I find the factors of larger numbers?
A: For larger numbers, systematic approaches such as trial division or prime factorization algorithms become necessary. Computer programs can efficiently find factors of very large numbers.
Conclusion
Understanding the factors of a number, particularly how they pair up and relate to prime factorization, is fundamental to various mathematical concepts. This article has explored the factors of 125, demonstrating the factor pairs (1 x 125 and 5 x 25), the prime factorization (5³), and the broader significance of factor pairs in simplifying fractions, solving equations, and understanding number theory. By systematically exploring the factors of 125, we gain a deeper appreciation for the structure and properties of numbers, laying a solid foundation for more advanced mathematical explorations. The principles discussed here are applicable to a wide range of numbers, highlighting the interconnectedness of mathematical concepts and their practical applications. Further exploration of divisibility rules and the use of algorithms for factoring larger numbers will enhance your proficiency in this vital area of mathematics.
Latest Posts
Latest Posts
-
Soda Ash In A Pool
Sep 16, 2025
-
What Numbers Go Into 21
Sep 16, 2025
-
Words To Describe My Daughter
Sep 16, 2025
-
Maharashtra State Board History Textbook
Sep 16, 2025
-
What Numbers Go Into 40
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factors Of 125 In Pairs . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.