Is 15 A Odd Number
seoindie
Sep 16, 2025 · 5 min read
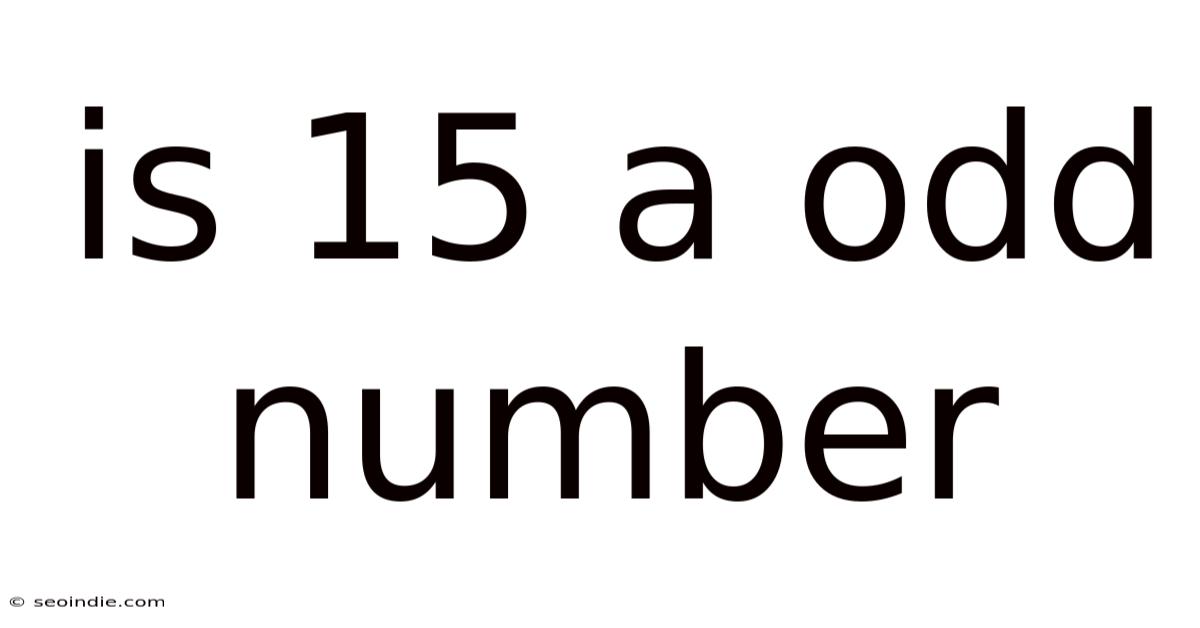
Table of Contents
Is 15 an Odd Number? A Deep Dive into Odd and Even Numbers
Is 15 an odd number? The answer, simply put, is yes. But understanding why 15 is odd goes beyond a simple yes or no. This seemingly straightforward question opens the door to exploring fundamental concepts in mathematics, including number theory, divisibility, and the properties of integers. This article will delve into the definition of odd and even numbers, explore the mathematical reasoning behind classifying 15 as odd, and address common misconceptions. We'll also touch on the broader implications of odd and even numbers in various mathematical fields.
Understanding Odd and Even Numbers: The Foundation
Before we definitively label 15, let's establish a clear understanding of what constitutes an odd and an even number. At its core, the distinction lies in divisibility by 2.
-
Even numbers are integers that are perfectly divisible by 2, leaving no remainder. This means they can be expressed as 2 * n, where 'n' is any integer (positive, negative, or zero). Examples include -4, 0, 2, 4, 6, 8, 10, and so on.
-
Odd numbers are integers that are not perfectly divisible by 2. When divided by 2, they leave a remainder of 1. They can be expressed as 2 * n + 1, where 'n' is again any integer. Examples include -3, -1, 1, 3, 5, 7, 9, 11, 13, 15, and so forth.
Why 15 is Unequivocally Odd
Now, let's apply this definition to the number 15. When we divide 15 by 2:
15 ÷ 2 = 7 with a remainder of 1.
This remainder of 1 immediately classifies 15 as an odd number. It cannot be expressed as 2 multiplied by an integer. The closest we can get is 2 * 7 = 14, which is one less than 15. Therefore, 15 perfectly fits the definition of an odd number: 2n + 1 (where n = 7).
Exploring the Properties of Odd Numbers
Odd numbers possess several interesting properties that set them apart from even numbers. These properties are crucial in various mathematical contexts, including algebra, number theory, and even cryptography. Let's examine a few:
-
Sum and Difference: The sum of two odd numbers is always an even number. For instance, 15 + 3 = 18. The difference between two odd numbers is always an even number. For example, 15 - 3 = 12. The sum of an odd and an even number is always odd. For example, 15 + 2 = 17. The difference between an odd and an even number is always odd. For example, 15 - 2 = 13.
-
Product: The product of two odd numbers is always an odd number. Multiplying 15 by any other odd number will always result in an odd number (e.g., 15 * 3 = 45, 15 * 5 = 75). However, the product of an odd number and an even number is always even.
-
Squares and Cubes: The square of an odd number is always odd (15² = 225). The cube of an odd number is always odd (15³ = 3375). This pattern continues for higher powers.
Odd Numbers in Advanced Mathematics
The seemingly simple distinction between odd and even numbers takes on significant importance in more advanced mathematical fields. Here are a few examples:
-
Number Theory: Concepts like prime numbers (numbers divisible only by 1 and themselves) and composite numbers (numbers with more than two divisors) are deeply intertwined with the properties of odd and even numbers. Many theorems and proofs in number theory rely on distinguishing between odd and even numbers.
-
Modular Arithmetic: In modular arithmetic (a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value called the modulus), the concept of odd and even numbers plays a critical role. This system is used extensively in cryptography and computer science.
-
Abstract Algebra: The concepts of oddness and evenness can be generalized and formalized within the framework of abstract algebra, where they contribute to the understanding of group theory and ring theory.
Addressing Common Misconceptions
While the concept of odd and even numbers is fundamental, some common misconceptions can arise:
-
Zero: Many people mistakenly believe zero is neither odd nor even. However, according to the mathematical definition, zero is an even number because it's divisible by 2 with a remainder of 0 (0 ÷ 2 = 0).
-
Negative Numbers: The concept of odd and even applies equally to negative numbers. Negative odd numbers (-1, -3, -5, etc.) and negative even numbers (-2, -4, -6, etc.) follow the same rules of divisibility by 2 as their positive counterparts.
Frequently Asked Questions (FAQ)
Q: Is there a way to easily identify odd numbers?
A: Yes. Odd numbers always end in 1, 3, 5, 7, or 9 in base 10. This is a quick visual check, although it doesn't work for other number bases.
Q: Are there infinitely many odd numbers?
A: Yes. For every even number, there's a corresponding odd number (just add 1). Since there are infinitely many integers, there are infinitely many odd and even numbers.
Q: What is the significance of odd and even numbers in real-world applications?
A: While not directly obvious in everyday life, the principles of odd and even numbers underpin many technologies. Examples include data compression algorithms, error detection codes, and various aspects of computer security.
Conclusion: 15's Unwavering Oddness
Returning to our initial question, the evidence is irrefutable: 15 is an odd number. This seemingly simple classification highlights the foundational importance of divisibility by 2 and underscores the rich mathematical properties associated with odd and even numbers. Their seemingly straightforward nature belies a depth of mathematical significance that extends far beyond basic arithmetic. Understanding odd and even numbers is not just about knowing whether 15 fits into one category or another; it's about grasping a fundamental concept that underpins numerous advanced mathematical concepts and real-world applications. From number theory to cryptography, the distinction between odd and even continues to be a vital building block in the vast and fascinating world of mathematics.
Latest Posts
Latest Posts
-
Hardest Tissue Of The Body
Sep 16, 2025
-
3 Meters How Many Inches
Sep 16, 2025
-
What Are Measures Of Dispersion
Sep 16, 2025
-
Is 3 0 A Whole Number
Sep 16, 2025
-
Factors Of 125 In Pairs
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 15 A Odd Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.