3 Times What Equals 60
seoindie
Sep 20, 2025 · 5 min read
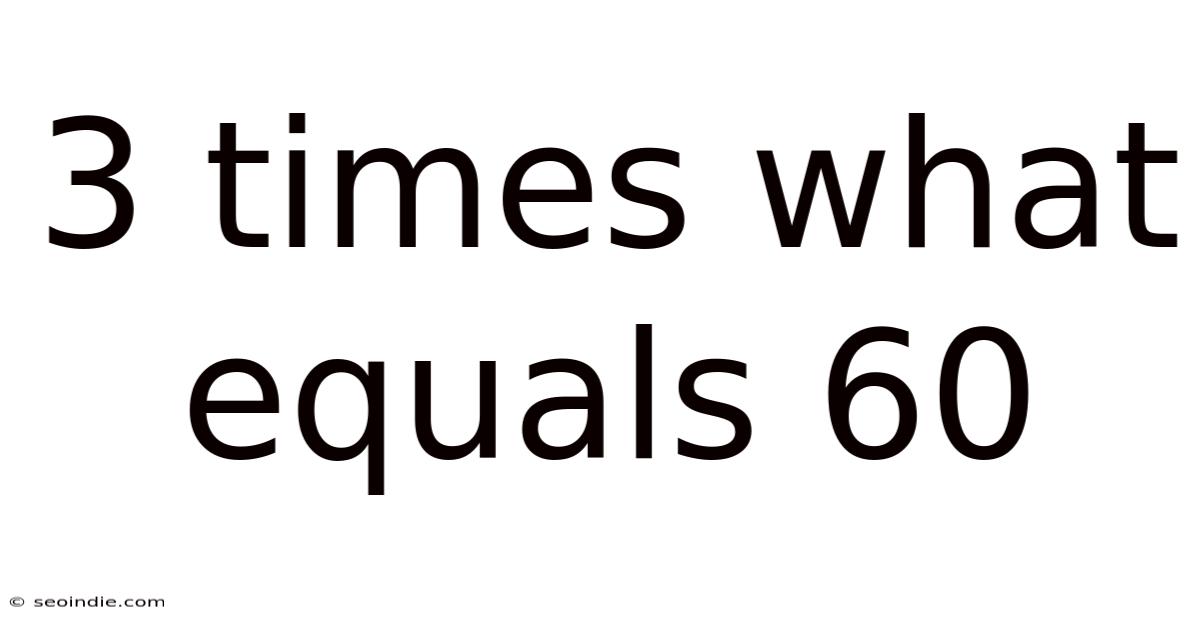
Table of Contents
Decoding the Mystery: 3 Times What Equals 60? A Deep Dive into Multiplication and Problem Solving
Finding the answer to "3 times what equals 60?" might seem simple at first glance. However, this seemingly straightforward question offers a fantastic opportunity to delve into the fundamentals of multiplication, explore different problem-solving approaches, and even touch upon more advanced mathematical concepts. This article will not only provide the answer but also equip you with the tools and understanding to tackle similar problems with confidence. We'll cover various methods, from basic arithmetic to algebraic solutions, making this a comprehensive guide for learners of all levels.
Understanding Multiplication: The Foundation
Before we tackle the specific problem, let's solidify our understanding of multiplication. Multiplication is essentially repeated addition. When we say "3 times 20," we mean adding 20 three times: 20 + 20 + 20 = 60. This basic principle forms the cornerstone of solving countless mathematical problems. Understanding this connection between addition and multiplication is crucial for grasping the concept thoroughly. It's not just about memorizing multiplication tables; it's about understanding the underlying process.
Method 1: The Intuitive Approach – Trial and Error
The simplest way to solve "3 times what equals 60?" is through trial and error. We can start by testing different numbers:
- 3 x 10 = 30 (Too low)
- 3 x 20 = 60 (Correct!)
This method works well for smaller numbers, allowing for a quick and intuitive solution. However, as the numbers get larger, this approach becomes less efficient and more prone to errors.
Method 2: The Division Method – A More Efficient Approach
A more systematic and efficient approach is using division. Since multiplication and division are inverse operations, we can find the unknown number by dividing 60 by 3:
60 ÷ 3 = 20
This method provides a direct and accurate solution regardless of the size of the numbers involved. It's a fundamental technique in arithmetic and forms the basis for solving more complex equations. It's important to remember that division is simply the process of finding out how many times one number goes into another.
Method 3: Algebraic Approach – Formalizing the Problem
For those familiar with algebra, we can express the problem as an equation:
3 * x = 60
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we isolate it by dividing both sides of the equation by 3:
3 * x / 3 = 60 / 3
This simplifies to:
x = 20
This algebraic approach provides a more formal and generalized method for solving similar problems. It's a crucial skill in higher-level mathematics and essential for tackling more complex equations.
Exploring Related Concepts: Factors, Multiples, and Divisibility
Solving "3 times what equals 60?" naturally leads us to explore related mathematical concepts:
-
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. In our example, 3 and 20 are factors of 60.
-
Multiples: Multiples are the results of multiplying a number by integers (whole numbers). 60 is a multiple of 3 and 20.
-
Divisibility Rules: Understanding divisibility rules can help quickly determine if a number is divisible by another. For example, a number is divisible by 3 if the sum of its digits is divisible by 3. In the case of 60, 6 + 0 = 6, which is divisible by 3, confirming that 60 is divisible by 3.
Extending the Concept: Real-World Applications
The seemingly simple problem of "3 times what equals 60?" has numerous real-world applications:
-
Shopping: If three identical items cost $60, how much does each item cost? (Answer: $20)
-
Baking: If a recipe calls for 3 cups of flour and you want to triple the recipe, how much flour do you need? (Answer: 9 cups)
-
Measurement: If three pieces of wood, each the same length, together measure 60 centimeters, what is the length of each piece? (Answer: 20 centimeters)
These examples illustrate the practical significance of understanding multiplication and problem-solving techniques. The ability to quickly and accurately solve such problems is a valuable skill in various aspects of life.
Expanding the Scope: Variations and Challenges
Let's consider variations of the original problem to further solidify our understanding:
-
What if the question was "3 times what equals 63?" Using division, we find that 63 ÷ 3 = 21.
-
What if the question involved decimals? For example, "3 times what equals 60.9?" The solution would be 60.9 ÷ 3 = 20.3.
-
What if the question was presented as a word problem requiring multiple steps? This would necessitate breaking down the problem into smaller, manageable parts, applying the same fundamental principles of multiplication and division.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to solve "3 times what equals 60?"
A: The quickest way is to use division: 60 ÷ 3 = 20.
Q: Are there other mathematical operations involved in solving this type of problem?
A: Primarily, division is the inverse operation used to solve for the unknown. However, an understanding of addition (as the foundation of multiplication) is also crucial.
Q: How can I improve my ability to solve similar problems quickly and accurately?
A: Practice is key. Regularly solving multiplication and division problems, gradually increasing the complexity, will significantly improve your skills. Also, focusing on understanding the underlying concepts rather than just memorizing facts is essential for long-term mastery.
Q: Can this type of problem be solved using a calculator?
A: Yes, a calculator can be used to perform the division (60 ÷ 3). However, understanding the underlying mathematical principles is still vital for problem-solving in more complex scenarios.
Conclusion: Mastering Multiplication and Beyond
The seemingly simple question "3 times what equals 60?" opens a door to a wide range of mathematical concepts and problem-solving techniques. From basic arithmetic to algebraic solutions, we've explored various approaches. The key takeaway isn't just the answer (20), but the understanding of the underlying principles: the relationship between multiplication and division, the importance of efficient methods like division, and the ability to apply these skills to various real-world situations. Mastering these fundamentals is crucial for success in mathematics and its various applications in everyday life. Continue practicing, explore related concepts, and you'll find yourself confidently tackling even more complex mathematical challenges.
Latest Posts
Latest Posts
-
What Times What Equals 76
Sep 20, 2025
-
How Tall Is 72 Cm
Sep 20, 2025
-
Calculating Percent Difference In Excel
Sep 20, 2025
-
Onion Cell Mitosis Answer Key
Sep 20, 2025
-
How To Find Atomic Size
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.