What Times What Equals 76
seoindie
Sep 20, 2025 · 5 min read
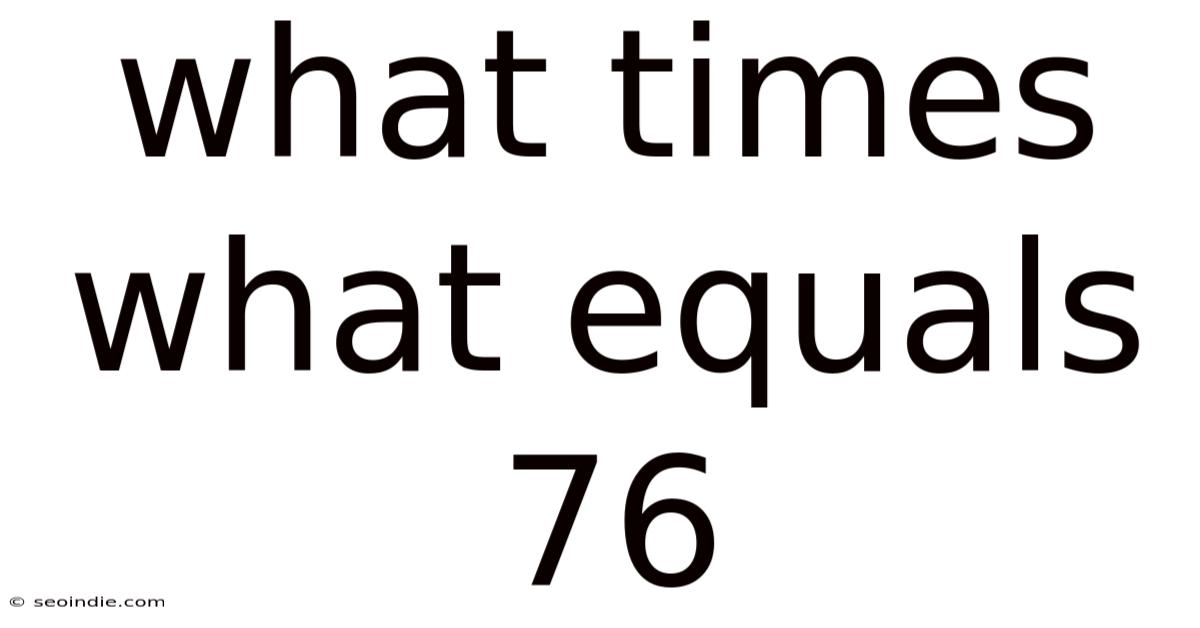
Table of Contents
What Times What Equals 76? Exploring the Factors and Prime Factorization of 76
Finding the numbers that multiply to equal 76 might seem like a simple arithmetic problem, but it opens a door to exploring fundamental concepts in mathematics, such as factors, prime factorization, and even the divisibility rules. This article delves deep into finding the answer, exploring the mathematical concepts involved, and extending the understanding beyond the simple solution. We'll even touch upon why understanding this seemingly simple problem is crucial for more advanced mathematical concepts.
Understanding Factors
Before we dive into solving "what times what equals 76," let's establish a clear understanding of factors. Factors are whole numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 perfectly. Finding the factors of a number is the first step in understanding its composition.
Finding the Factors of 76: A Step-by-Step Approach
To find the pairs of numbers that multiply to 76, we can systematically check each whole number starting from 1.
-
Start with 1: 1 x 76 = 76. Therefore, 1 and 76 are a factor pair.
-
Check for divisibility by 2: Since 76 is an even number (ends in 6), it's divisible by 2. 76 / 2 = 38. So, 2 and 38 are another factor pair.
-
Check for divisibility by 3: The divisibility rule for 3 states that the sum of the digits must be divisible by 3. 7 + 6 = 13, which is not divisible by 3. Therefore, 3 is not a factor.
-
Check for divisibility by 4: The divisibility rule for 4 states that the last two digits must be divisible by 4. Since 76 is divisible by 4 (76 / 4 = 19), 4 and 19 are a factor pair.
-
Check for divisibility by 5: Numbers divisible by 5 end in 0 or 5. 76 doesn't end in 0 or 5, so 5 is not a factor.
-
Check for divisibility by other numbers: We continue checking numbers until we reach the square root of 76 (approximately 8.7). Since we've already found 4 and 19, and the next number (6) doesn’t work, we can stop our systematic search. We've identified all factor pairs.
The Factor Pairs of 76
Therefore, the pairs of numbers that multiply to 76 are:
- 1 x 76
- 2 x 38
- 4 x 19
These are all the possible combinations of whole numbers that result in a product of 76.
Prime Factorization: Unveiling the Building Blocks
Prime factorization breaks down a number into its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization provides a unique representation of a number, regardless of the order of the factors.
To find the prime factorization of 76, we can use a factor tree:
76
/
2 38
/
2 19
The prime factorization of 76 is 2 x 2 x 19, or 2² x 19. This means that 76 is built solely from the prime numbers 2 and 19. This representation is fundamental in various areas of mathematics, including simplifying fractions and understanding the properties of numbers.
Practical Applications and Real-World Examples
While seemingly basic, understanding factors and prime factorization has far-reaching applications:
-
Simplifying Fractions: When reducing fractions, finding common factors is essential. Understanding the prime factorization of the numerator and denominator allows for efficient simplification.
-
Algebra: Factoring polynomials relies heavily on the ability to identify factors. This is a cornerstone skill in higher-level algebra.
-
Cryptography: Prime numbers play a crucial role in cryptography, the science of secure communication. Many encryption methods rely on the difficulty of factoring very large numbers into their prime components.
-
Number Theory: Number theory, a branch of pure mathematics, explores the properties of numbers, with prime factorization forming the basis of many theorems and proofs.
-
Data Structures and Algorithms: In computer science, understanding factors can be applied in optimizing algorithms and improving efficiency of data structures.
Frequently Asked Questions (FAQ)
-
Q: Are there any negative factor pairs for 76? A: Yes, -1 x -76, -2 x -38, and -4 x -19 also equal 76. When dealing with multiplication, two negative numbers result in a positive product.
-
Q: Is there only one prime factorization for 76? A: Yes, the prime factorization of a number is unique (ignoring the order of the factors). This is a fundamental theorem of arithmetic.
-
Q: How do I find factors of larger numbers? A: For larger numbers, systematic checking becomes tedious. Algorithms and software can help, but understanding divisibility rules and prime factorization remain key concepts.
Conclusion: Beyond the Simple Answer
The simple answer to "what times what equals 76?" is a set of factor pairs: 1 x 76, 2 x 38, and 4 x 19 (and their negative counterparts). However, this seemingly simple problem provides a gateway to understanding the rich world of factors, prime factorization, and their profound implications in mathematics and beyond. By exploring these concepts, we move beyond rote memorization and develop a deeper, more intuitive understanding of numbers and their relationships. This understanding forms a solid foundation for tackling more complex mathematical challenges in the future. The seemingly simple question of "what times what equals 76?" becomes a springboard for mathematical exploration and a demonstration of how foundational concepts underlie more advanced mathematical principles. This underscores the importance of mastering basic mathematical principles to build a stronger understanding of higher-level concepts.
Latest Posts
Latest Posts
-
Words With P And F
Sep 20, 2025
-
Water Freezing And Boiling Point
Sep 20, 2025
-
Lcm Of 6 And 7
Sep 20, 2025
-
Words That Rhyme With Bun
Sep 20, 2025
-
12 Class Math Book Pdf
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.