10 Square Root Of 3
seoindie
Sep 15, 2025 · 6 min read
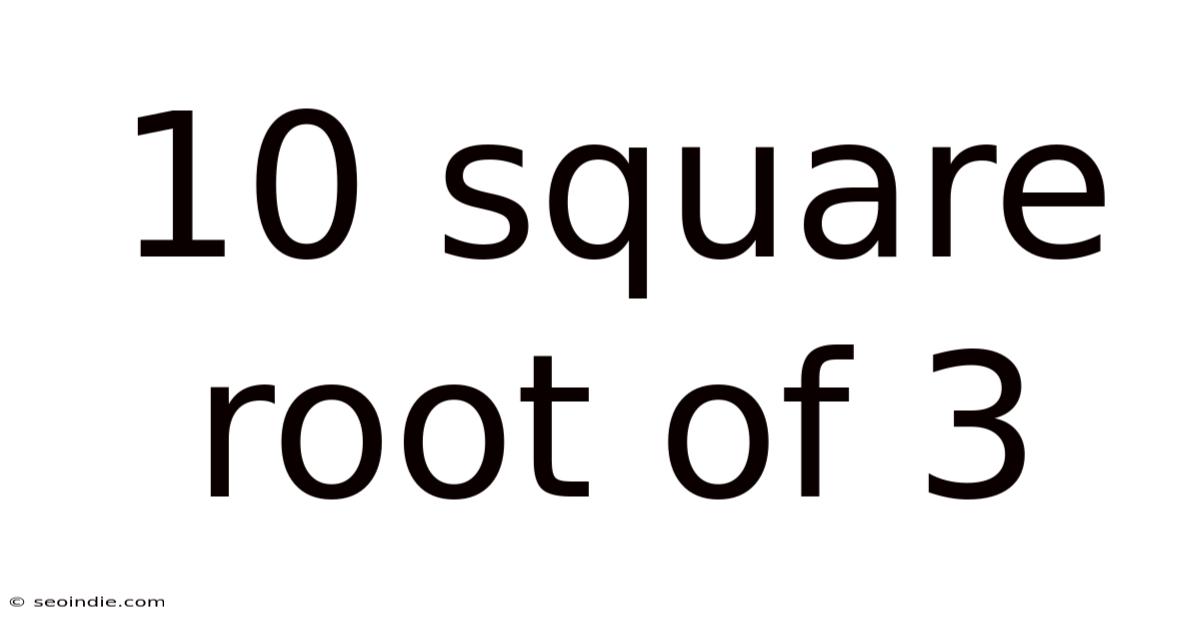
Table of Contents
Unveiling the Mysteries of 10√3: A Deep Dive into its Properties and Applications
Understanding the square root of 3 (√3) and its multiples is fundamental in various fields, from basic geometry and trigonometry to advanced physics and engineering. This article provides a comprehensive exploration of 10√3, explaining its properties, calculations, applications, and significance in different contexts. We'll delve into its geometric representation, approximations, and its role in solving real-world problems, ensuring a thorough understanding for readers of all levels. This exploration will cover not only the numerical value but also its practical implications, making the concept of 10√3 accessible and engaging.
Understanding the Basics: Square Roots and √3
Before delving into the specifics of 10√3, let's refresh our understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. The square root of 3 (√3), however, is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating.
The approximate value of √3 is 1.732. This is an approximation, as the actual value has an infinite number of decimal places. Understanding this irrational nature is crucial when working with calculations involving √3.
Calculating 10√3: Methods and Approximations
Calculating 10√3 is straightforward: we simply multiply the approximate value of √3 by 10.
- Using the approximate value: 10 * 1.732 ≈ 17.32
This gives us a reasonably accurate approximation. However, the precision depends on the number of decimal places used for √3. Using a more precise value of √3 will yield a more accurate result for 10√3.
-
Using a calculator: Most scientific calculators have a square root function (√). Simply enter √3, multiply by 10, and the calculator will provide a more precise approximation, often to several decimal places.
-
Geometric Approach: While not a direct calculation method, the geometric representation of 10√3 provides valuable insight. Consider an equilateral triangle with sides of length 10. The height of this triangle is precisely 10√3/2, or 5√3. This geometric interpretation illustrates the practical application of this value in calculating lengths and areas.
Geometric Applications of 10√3
The value 10√3 frequently appears in geometry problems. Let's explore some key examples:
-
Equilateral Triangles: As mentioned above, in an equilateral triangle with side length 10, the height is 5√3. Therefore, the area of this triangle is (1/2) * base * height = (1/2) * 10 * 5√3 = 25√3. This illustrates how 10√3, or its factors, appear in area calculations.
-
30-60-90 Triangles: This special right triangle has angles of 30°, 60°, and 90°. If the hypotenuse has length 20, the side opposite the 60° angle will be 10√3, and the side opposite the 30° angle will be 10. This relationship is crucial in trigonometry and geometric problem-solving.
-
Hexagons: A regular hexagon can be divided into six equilateral triangles. If the side length of the hexagon is 10, then its area can be calculated using the area of the constituent equilateral triangles, which, as we've seen, involves 10√3.
Trigonometric Applications of 10√3
Trigonometry frequently utilizes √3, and consequently, multiples like 10√3.
-
Special Angles: The value of √3 appears in the trigonometric ratios of special angles like 60° and 30°. For example, tan(60°) = √3 and sin(60°) = √3/2. These relationships, when incorporated into problems involving angles, will often lead to expressions containing 10√3.
-
Vector Analysis: In vector calculations involving angles and magnitudes, √3, and consequently 10√3, often appear in calculations involving components of vectors.
-
Complex Numbers: In the context of complex numbers, the value √3 appears in the representation of complex numbers in polar form, further contributing to its appearance in various mathematical applications.
Advanced Applications: Physics and Engineering
Beyond basic geometry and trigonometry, 10√3 and its related values find application in more advanced fields:
-
Physics: In physics, particularly in mechanics and electricity, calculations involving vectors, forces, and fields often lead to expressions involving √3, and therefore, its multiples. For example, in resolving forces acting at an angle, we might encounter values involving 10√3.
-
Engineering: Civil and mechanical engineering designs frequently utilize geometric principles. Calculations related to structural stability, stress analysis, and material properties often incorporate √3 and its multiples, making 10√3 a relevant value in engineering calculations.
-
Computer Graphics: In computer graphics, the manipulation of 2D and 3D objects often relies on trigonometric and geometric principles. The efficient calculation and manipulation of objects requires an understanding of values like 10√3 for accurate rendering and transformation.
Approximations and Error Analysis
It is important to understand the limitations of using approximate values for √3 and consequently for 10√3. The precision of the result depends directly on the number of decimal places used in the approximation. For most practical applications, using 1.732 for √3 provides sufficient accuracy. However, in applications demanding high precision, more decimal places should be used, or the exact value √3 should be retained throughout the calculations, using a symbolic math software or calculator. Understanding the potential error introduced by using approximations is crucial for accurate results.
Frequently Asked Questions (FAQ)
Q: What is the exact value of 10√3?
A: There is no exact decimal representation for 10√3, as √3 is an irrational number. It can only be expressed as 10 times the square root of 3.
Q: How do I calculate 10√3 without a calculator?
A: You can use a long division method to approximate the square root of 3, and then multiply the result by 10. However, this method is tedious and prone to errors. Using a table of square roots, or a calculator, is recommended for practical purposes.
Q: What are the units associated with 10√3?
A: The units associated with 10√3 depend on the context. If it represents a length, the units could be meters, centimeters, feet, etc. If it represents an area, the units could be square meters, square centimeters, etc.
Q: Can 10√3 be simplified further?
A: No, 10√3 is already in its simplest form. The 10 is an integer, and √3 is an irrational number that cannot be simplified.
Conclusion
10√3, while seemingly a simple mathematical expression, represents a significant concept with far-reaching applications across various disciplines. From basic geometry and trigonometry to advanced fields like physics and engineering, understanding its properties and methods of calculation is crucial. This article aimed to provide a thorough exploration of 10√3, highlighting its properties, calculations, applications, and the importance of accurate approximations. By grasping the fundamentals presented here, readers can confidently approach problems involving this important mathematical constant and appreciate its role in solving real-world problems. Remember, the key to mastering this concept lies in understanding the underlying principles of square roots, geometry, and trigonometry, and applying them effectively in various contexts.
Latest Posts
Latest Posts
-
What Numbers Go Into 75
Sep 16, 2025
-
What Is 99 Divisible By
Sep 16, 2025
-
Lcm Of 8 12 15
Sep 16, 2025
-
How Long Is 13 Cm
Sep 16, 2025
-
Lcm Of 2 And 5
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 10 Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.