Lcm Of 2 And 5
seoindie
Sep 11, 2025 · 6 min read
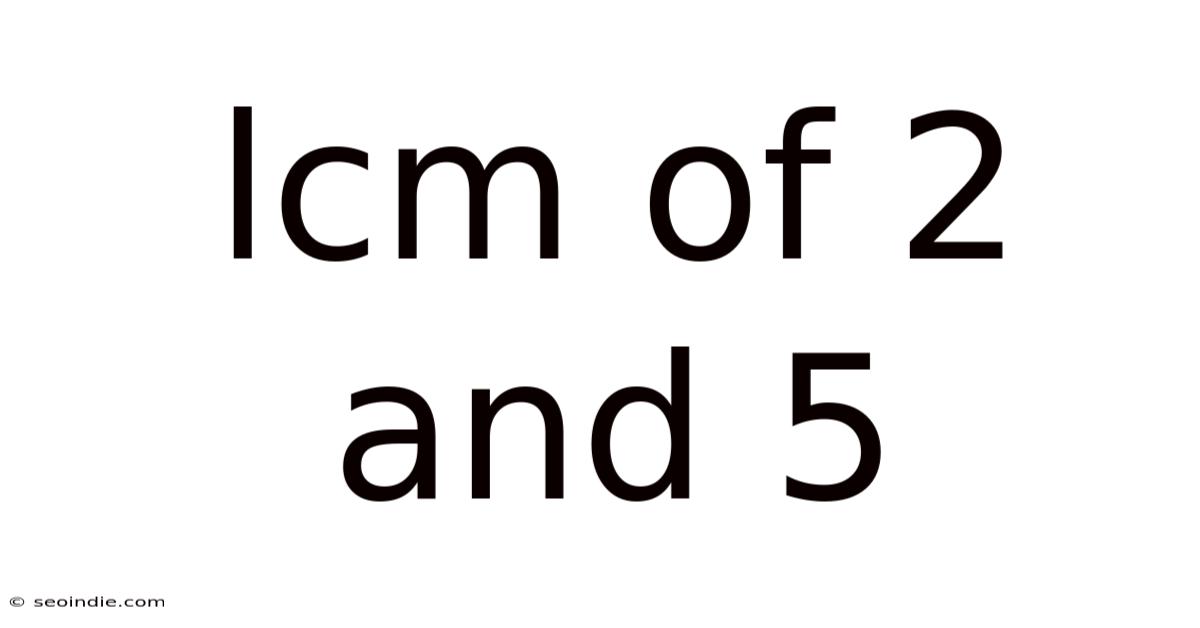
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 5: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts provides a strong foundation for more advanced mathematics. This article will delve into the LCM of 2 and 5, exploring various methods to calculate it, its applications in real-world scenarios, and its connection to other mathematical concepts like the greatest common divisor (GCD). We will also explore how to find the LCM of larger numbers and discuss the significance of prime factorization in this process. By the end, you'll have a comprehensive understanding of LCM, extending far beyond just finding the answer for 2 and 5.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. For instance, if we consider the numbers 2 and 5, the LCM is the smallest number that is divisible by both 2 and 5.
Understanding the LCM is crucial in various mathematical contexts, from simplifying fractions to solving problems in algebra and number theory. Its applications extend to real-world situations, such as scheduling events that occur at regular intervals or determining the size of equally sized groups from objects of different quantities.
Methods to Find the LCM of 2 and 5
There are several ways to determine the LCM of 2 and 5. Let's explore the most common methods:
1. Listing Multiples:
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
The smallest multiple that appears in both lists is 10. Therefore, the LCM of 2 and 5 is 10.
2. Prime Factorization:
This method is more efficient for larger numbers. We find the prime factorization of each number and then identify the highest power of each prime factor present in either factorization. The LCM is the product of these highest powers.
- Prime factorization of 2: 2¹
- Prime factorization of 5: 5¹
The prime factors are 2 and 5. The highest power of 2 is 2¹, and the highest power of 5 is 5¹. Therefore, the LCM is 2¹ * 5¹ = 10.
3. Using the Formula: LCM(a, b) = (|a * b|) / GCD(a, b)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD of two numbers is the largest number that divides both without leaving a remainder.
- GCD of 2 and 5: The only positive integer that divides both 2 and 5 is 1. Therefore, GCD(2, 5) = 1.
- Applying the formula: LCM(2, 5) = (|2 * 5|) / GCD(2, 5) = 10 / 1 = 10
Real-World Applications of LCM
The LCM finds practical applications in numerous situations:
-
Scheduling: Imagine you have two events: one occurs every 2 days and the other every 5 days. To find when both events will occur on the same day, you need to find the LCM(2, 5) = 10. Both events will coincide every 10 days.
-
Pattern Repetition: Consider two repeating patterns. One pattern repeats every 2 units, and the other repeats every 5 units. The LCM helps determine when both patterns will align perfectly. This is useful in various fields like textile design, music composition, and even computer programming.
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator, simplifying the calculation.
-
Dividing Objects into Equal Groups: If you have 10 apples and you want to divide them equally among groups of 2 or 5 apples, the LCM(2, 5) = 10 tells you that you can divide them into 5 groups of 2 apples each, or 2 groups of 5 apples each.
Extending the Concept: LCM of Larger Numbers
While the listing multiples method is convenient for smaller numbers like 2 and 5, it becomes less practical for larger numbers. The prime factorization method proves more efficient. Let's find the LCM of 12 and 18:
- Prime factorization of 12: 2² * 3¹
- Prime factorization of 18: 2¹ * 3²
The highest power of 2 is 2², and the highest power of 3 is 3². Therefore, LCM(12, 18) = 2² * 3² = 4 * 9 = 36.
The Relationship Between LCM and GCD
The LCM and GCD are closely related. For any two positive integers a and b, the product of their LCM and GCD is equal to the product of the numbers themselves:
LCM(a, b) * GCD(a, b) = a * b
This relationship provides an alternative way to calculate the LCM if the GCD is known. For instance, in our example of 2 and 5, we know GCD(2, 5) = 1. Therefore:
LCM(2, 5) = (2 * 5) / GCD(2, 5) = 10 / 1 = 10
Frequently Asked Questions (FAQ)
Q: Is the LCM always larger than the two numbers?
A: Not always. If one number is a multiple of the other, the LCM will be equal to the larger number. For example, LCM(2, 4) = 4.
Q: Can the LCM of two numbers be negative?
A: No, the LCM is always a positive integer.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. The LCM will be the product of these highest powers. For example, to find the LCM of 4, 6, and 15:
- 4 = 2²
- 6 = 2¹ * 3¹
- 15 = 3¹ * 5¹
LCM(4, 6, 15) = 2² * 3¹ * 5¹ = 60
Q: What if the two numbers have no common factors other than 1?
A: If the GCD of two numbers is 1 (meaning they are relatively prime or coprime), then their LCM is simply the product of the two numbers. This is the case with 2 and 5.
Conclusion
Understanding the least common multiple is a fundamental concept in mathematics with far-reaching applications. While finding the LCM of 2 and 5 is relatively straightforward, the underlying principles and methods extend to more complex calculations. By mastering the different methods – listing multiples, prime factorization, and utilizing the relationship with the GCD – you equip yourself with the tools to tackle LCM problems effectively, regardless of the numbers involved. Remember that the key is to grasp the underlying mathematical concepts, allowing you to approach and solve even the most challenging problems with confidence and clarity. This deep understanding not only helps with direct applications but also strengthens your foundation for more advanced mathematical studies.
Latest Posts
Latest Posts
-
Glacial Acetic Acid Boiling Point
Sep 11, 2025
-
Words That Start With We
Sep 11, 2025
-
Words That Start With Bal
Sep 11, 2025
-
2 3 As A Mixed Number
Sep 11, 2025
-
Is Peach A Pure Substance
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.