Lcm Of 8 12 15
seoindie
Sep 16, 2025 · 6 min read
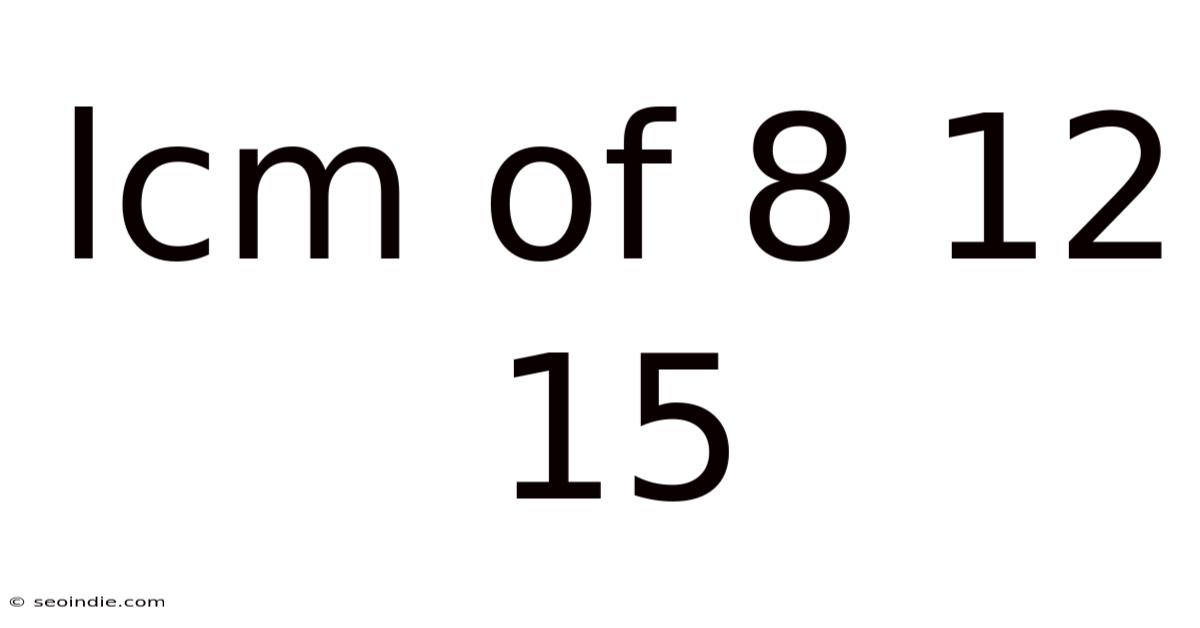
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 12, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for solving various problems in algebra, arithmetic, and even real-world scenarios involving scheduling and measurement. This article provides a comprehensive guide to calculating the LCM of 8, 12, and 15, exploring multiple methods and explaining the underlying mathematical principles. We'll delve into the concepts of prime factorization, the greatest common divisor (GCD), and provide practical examples to solidify your understanding. By the end, you'll not only know the LCM of 8, 12, and 15 but also possess the skills to calculate the LCM of any set of numbers.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
This concept is critical in various applications. Imagine you're organizing a cycling event, and three cyclists complete a lap in 8, 12, and 15 minutes respectively. The LCM will tell you the shortest time when all three cyclists will again arrive at the starting point simultaneously. This is just one of countless real-world examples illustrating the practical utility of LCM.
Method 1: Prime Factorization Method
This is arguably the most common and conceptually clearest method for finding the LCM. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply to give the original number. Let's apply this method to find the LCM of 8, 12, and 15:
1. Prime Factorization:
- 8: 2 x 2 x 2 = 2³
- 12: 2 x 2 x 3 = 2² x 3
- 15: 3 x 5
2. Identifying the Highest Powers:
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ (from the factorization of 8).
- The highest power of 3 is 3¹ (from the factorization of 12 and 15).
- The highest power of 5 is 5¹ (from the factorization of 15).
3. Calculating the LCM:
To find the LCM, we multiply these highest powers together:
LCM(8, 12, 15) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the least common multiple of 8, 12, and 15 is 120. This means that 120 is the smallest positive integer divisible by 8, 12, and 15.
Method 2: Listing Multiples Method
This method is simpler for smaller numbers but can become cumbersome with larger numbers. It involves listing the multiples of each number until you find the smallest multiple common to all.
1. Listing Multiples:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135...
2. Identifying the LCM:
The smallest multiple that appears in all three lists is 120. Therefore, the LCM(8, 12, 15) = 120.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
While this formula is primarily used for two numbers, we can extend it to multiple numbers by applying it iteratively. First, we find the GCD of two numbers, then use the result to find the GCD of the next number, and so on. This method is less intuitive for beginners but highlights the mathematical relationship between LCM and GCD.
1. Finding the GCD of 8 and 12:
Using the Euclidean algorithm (a common method for finding the GCD), we get:
12 = 1 x 8 + 4 8 = 2 x 4 + 0
The GCD(8, 12) = 4.
2. Finding the GCD of the result (4) and 15:
Since 4 and 15 have no common factors other than 1, GCD(4, 15) = 1.
3. Using the LCM and GCD Relationship (for two numbers at a time):
-
LCM(8,12) * GCD(8,12) = 8 * 12
-
LCM(8,12) * 4 = 96
-
LCM(8,12) = 24
-
LCM(24,15) * GCD(24,15) = 24 * 15
-
LCM(24,15) * 1 = 360
-
LCM(24,15) = 120
Therefore, LCM(8,12,15) = 120. Note that this iterative approach is less straightforward than prime factorization, especially with more than two numbers.
Why is Understanding LCM Important?
Understanding LCM isn't just about solving math problems; it's about developing a deeper appreciation for mathematical relationships and their application in real-world scenarios. Here are some key reasons why understanding LCM is important:
-
Problem Solving: LCM is essential for solving various problems involving fractions, ratios, and proportions. It helps find common denominators when adding or subtracting fractions.
-
Scheduling and Timing: As shown in the cycling example, LCM helps determine when events will coincide. This is valuable in scheduling tasks, coordinating meetings, or understanding cyclical processes.
-
Measurement and Units: LCM is vital when working with different units of measurement. For example, if you need to measure lengths using rulers with different markings (say, 8cm, 12cm, and 15cm), knowing the LCM helps determine the smallest common length that can be measured precisely by all rulers.
-
Modular Arithmetic: LCM plays a significant role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Abstract Algebra: The concept of LCM extends to more advanced mathematical structures like rings and fields, forming the basis for more complex algebraic concepts.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have common factors?
A1: If the numbers share common factors, the LCM will be smaller than the product of the numbers. The prime factorization method automatically accounts for common factors by only considering the highest powers of each prime factor.
Q2: Can I use a calculator to find the LCM?
A2: Many scientific calculators and online calculators have built-in functions to calculate the LCM of multiple numbers. However, understanding the underlying methods is crucial for developing a strong mathematical foundation.
Q3: What is the difference between LCM and GCD?
A3: The least common multiple (LCM) is the smallest positive integer that is a multiple of all the numbers in a set. The greatest common divisor (GCD) is the largest positive integer that divides all the numbers in a set. They are inversely related; a larger GCD means a smaller LCM, and vice versa.
Q4: How do I find the LCM of more than three numbers?
A4: You can extend the prime factorization method to any number of integers. Find the prime factorization of each number, identify the highest power of each prime factor, and then multiply those highest powers together to get the LCM.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with widespread applications. While various methods exist, the prime factorization method offers a clear, systematic approach suitable for numbers of any size. Understanding the concept of LCM isn't just about calculating a number; it's about mastering a crucial mathematical tool that can enhance your problem-solving skills and deepen your comprehension of numerical relationships. Through this comprehensive guide, you’ve not only learned how to calculate the LCM of 8, 12, and 15 (which is 120) but also gained a broader understanding of the concept and its practical significance across various mathematical domains and real-world applications. Remember to practice regularly, exploring different methods and applying the concept to various problems to solidify your understanding.
Latest Posts
Latest Posts
-
Is 4 A Irrational Number
Sep 16, 2025
-
Square And Square Root Table
Sep 16, 2025
-
How Do You Spell 2500
Sep 16, 2025
-
Whats The Factors Of 18
Sep 16, 2025
-
Differentiate Between Euchromatin And Heterochromatin
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.