1 9/100 As A Percent
seoindie
Sep 23, 2025 · 5 min read
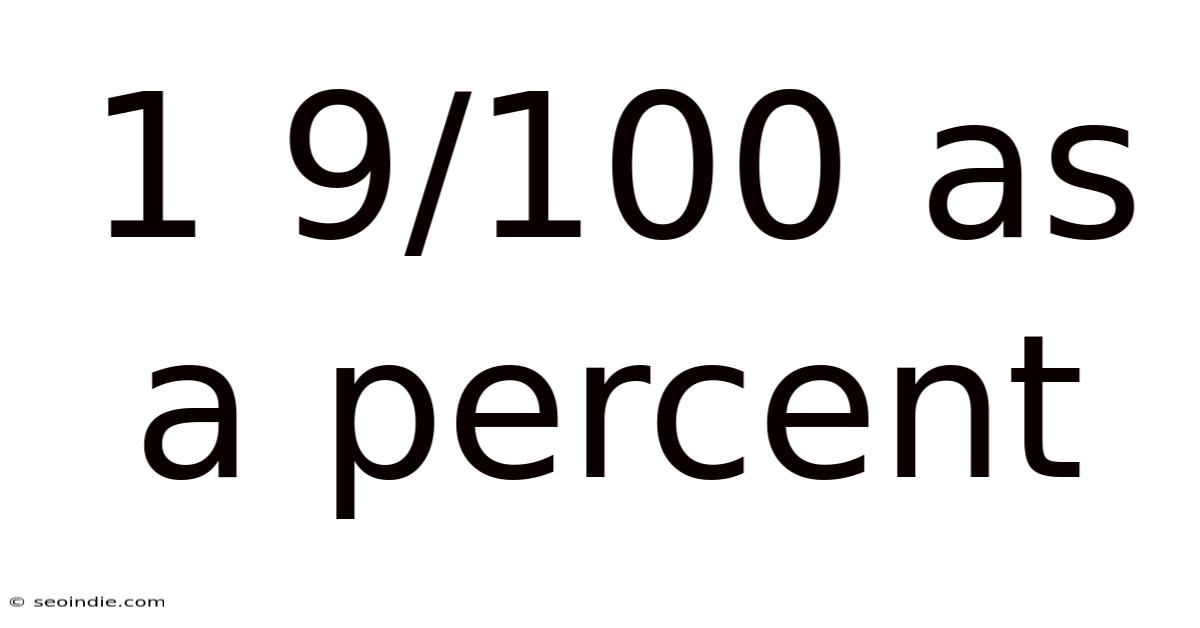
Table of Contents
1/9/100 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This article will comprehensively guide you through the process of converting the fraction 1/9/100 into a percentage, explaining each step in detail and addressing common misunderstandings along the way. We'll delve into the underlying mathematical principles, providing a solid foundation for tackling similar conversions in the future. By the end, you'll not only know the answer but also understand the "why" behind the calculation.
Understanding the Components: Fractions, Decimals, and Percentages
Before we dive into the conversion, let's refresh our understanding of the three key components:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator.
-
Decimals: A decimal is a way of expressing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.5 is a decimal representation of one-half (1/2).
-
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol % is used to represent percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Interpreting 1/9/100
The expression "1/9/100" is ambiguous. It could be interpreted in two ways:
-
As a complex fraction: This interpretation means (1/9)/100. This is a fraction divided by another number.
-
As a product of fractions: This interpretation means (1/9) * (1/100). This is the multiplication of two fractions.
We will address both interpretations to ensure complete understanding.
Interpretation 1: (1/9)/100 as a Percentage
This interpretation involves a complex fraction. Let's break down the conversion step by step:
Step 1: Simplify the complex fraction.
To simplify (1/9)/100, we can rewrite 100 as 100/1:
(1/9) / (100/1)
Now, remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 100/1 is 1/100. Therefore:
(1/9) * (1/100) = 1/900
Step 2: Convert the fraction to a decimal.
To convert 1/900 to a decimal, we perform the division:
1 ÷ 900 ≈ 0.0011111...
The result is a recurring decimal.
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply by 100 and add the % symbol:
0.0011111... * 100 ≈ 0.11111...%
Therefore, (1/9)/100 expressed as a percentage is approximately 0.1111%.
Interpretation 2: (1/9) * (1/100) as a Percentage
This interpretation involves the multiplication of two fractions. Let's proceed with the conversion:
Step 1: Multiply the fractions.
(1/9) * (1/100) = 1/900
This yields the same fraction as in Interpretation 1.
Step 2: Convert the fraction to a decimal.
As before, we perform the division:
1 ÷ 900 ≈ 0.0011111...
Step 3: Convert the decimal to a percentage.
Multiplying the decimal by 100 and adding the percentage symbol:
0.0011111... * 100 ≈ 0.11111...%
Again, we arrive at approximately 0.1111%.
Understanding Recurring Decimals
In both interpretations, we encountered a recurring decimal (0.0011111...). This means the digit 1 repeats infinitely. In practical applications, we usually round the decimal to a certain number of decimal places. For example, rounding to four decimal places gives us 0.0011, and to two decimal places gives 0.00%. The level of precision needed depends on the context of the problem.
Further Exploration: Applying Percentage Calculations
Understanding how to convert fractions to percentages is crucial in many real-world scenarios. Here are a few examples:
-
Financial Calculations: Calculating interest rates, discounts, or tax amounts often involves working with percentages.
-
Data Analysis: Percentages are essential for representing data proportions in charts, graphs, and reports.
-
Probability and Statistics: Percentages are used to express probabilities and frequencies in statistical analysis.
-
Everyday Life: Understanding percentages helps in comparing prices, calculating tips, or understanding discounts.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a fraction, decimal, and percentage?
A fraction represents a part of a whole as a ratio of two numbers. A decimal represents a number using a base-ten system with a decimal point. A percentage represents a fraction of 100.
Q2: Why did we get a recurring decimal in this calculation?
The recurring decimal arises because the fraction 1/900 has a denominator (900) that is not easily divisible by powers of 10. When converted to a decimal, it results in a non-terminating repeating decimal.
Q3: How can I convert any fraction to a percentage?
To convert any fraction to a percentage, first divide the numerator by the denominator to obtain a decimal. Then, multiply the decimal by 100 and add the % sign.
Q4: Is there a difference in the final answer if we round the decimal at different stages of the calculation?
Rounding at different stages can slightly alter the final answer. It's best to carry out the calculations with as much precision as possible and round only at the very end, based on the required level of accuracy.
Q5: How do I handle more complex fractions involving multiple layers?
For complex fractions with multiple layers, always simplify them step-by-step, following the order of operations (PEMDAS/BODMAS). Remember to address any brackets or parentheses first, then exponents, followed by multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Conclusion
Converting 1/9/100 to a percentage requires careful interpretation of the expression and a step-by-step approach. Whether interpreted as a complex fraction or a product of fractions, the result is approximately 0.1111%. Understanding the processes of converting between fractions, decimals, and percentages is essential for numerous applications across various fields. This article has provided a detailed breakdown of the process, addressing common questions and encouraging a deeper understanding of the underlying mathematical concepts. Remember to always check the context to determine the appropriate level of precision when rounding recurring decimals. By mastering these skills, you will be well-equipped to tackle similar percentage calculations with confidence.
Latest Posts
Latest Posts
-
1 2 N 1 N
Sep 23, 2025
-
Words Beginning With A H
Sep 23, 2025
-
Gcf Of 16 And 4
Sep 23, 2025
-
Definition Of Demand Pull Inflation
Sep 23, 2025
-
Define Order Of A Reaction
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 9/100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.