1 2 N 1 N
seoindie
Sep 23, 2025 · 6 min read
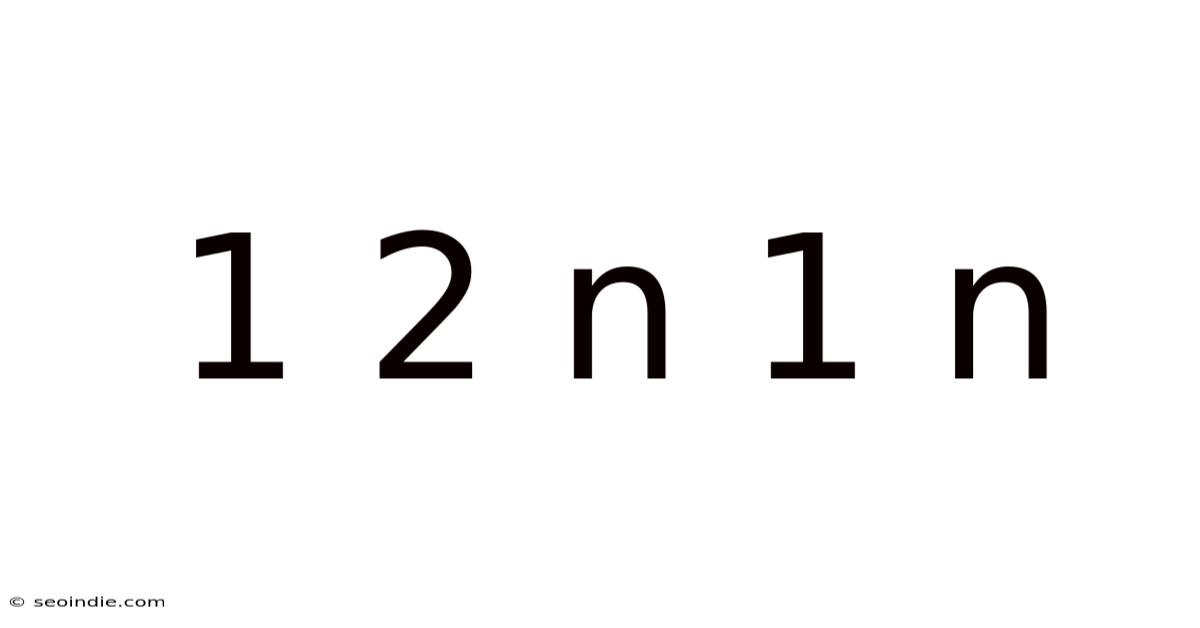
Table of Contents
Decoding the Mystery: A Deep Dive into the Sequence 1, 2, n, 1, n
The sequence 1, 2, n, 1, n might seem deceptively simple at first glance. However, understanding its implications requires exploring various mathematical and logical contexts. This seemingly straightforward sequence opens doors to discussions about pattern recognition, number theory, algorithm design, and even potential applications in fields like cryptography and coding theory. This article aims to provide a comprehensive understanding of this sequence, exploring its underlying structure, potential interpretations, and broader significance.
Understanding the Sequence: Initial Observations
The sequence 1, 2, n, 1, n presents a unique challenge because the 'n' acts as a wildcard. Unlike sequences with fixed values, this sequence's behavior is entirely dependent on the value assigned to 'n'. This immediately introduces the concept of parametric sequences, where the sequence's structure is defined but its specific terms depend on a variable.
Let's consider a few examples to illustrate:
- If n = 3: The sequence becomes 1, 2, 3, 1, 3. This is a finite sequence with five terms.
- If n = 5: The sequence becomes 1, 2, 5, 1, 5. Again, a finite sequence with five terms.
- If n = 100: The sequence becomes 1, 2, 100, 1, 100. A finite sequence with five terms.
Notice a pattern emerging. Regardless of the value of 'n', the sequence always contains five terms, with the 'n' value appearing twice. This consistent structure provides a foundation for further analysis.
Potential Interpretations and Applications
The sequence's simplicity belies its potential for diverse applications. Let's explore some possible interpretations:
-
As a Simple Code or Cipher: Imagine 'n' representing a secret key. The sequence could be a rudimentary cryptographic key exchange, where the initial '1' and '2' act as markers, and the repeated 'n' represents the encrypted data. This is, of course, a highly simplified example, vulnerable to many cryptanalytic attacks, but demonstrates the potential for applying such sequences in security.
-
Representing a State Transition Diagram: In computer science, state transition diagrams visually represent the different states a system can be in and the transitions between them. The sequence 1, 2, n, 1, n could potentially represent a simplified state machine. '1' and '2' could represent initial states, 'n' a particular state reached during the process, returning back to '1' and then finally 'n'. This allows for a simple representation of a process with repeated steps.
-
Modeling a Simple Process: The sequence might represent a simplified process where the first step is always 1, the second step 2, and the steps 'n' and 'n' are repeated. This could be conceptualized in many different real-world scenarios depending on the value of 'n'. For instance, if 'n' represents a certain amount of time, the sequence might represent a two-part process with a repeating step in between.
-
Mathematical Function Representation: Although it's not a standard mathematical function, it can represent a piecewise function depending on the value of 'n' and the desired outcome. Each element of the sequence could correspond to a particular step or value based on a set of rules. This approach allows for flexibility and opens up possibilities for unique mathematical representations.
-
Generating Sets: The sequence could serve as a base for generating sets. For instance, for a specific value of 'n', you could generate a set of sequences based on permutations or variations of the base sequence. This opens possibilities for combinatorial analysis and set theory applications.
Mathematical Analysis: Exploring Patterns and Relationships
While the sequence itself doesn't directly lead to complex mathematical formulas, its structure encourages exploration of underlying mathematical concepts.
-
Arithmetic Progression?: No, it's not a simple arithmetic progression. The common difference isn't constant. Arithmetic progressions have a consistent difference between consecutive terms.
-
Geometric Progression?: Again, no. Geometric progressions have a constant ratio between consecutive terms. This sequence lacks this consistency.
-
Recursive Relations?: The sequence can be partially described recursively, but not completely. While we can define the first two terms (1, 2), defining the third term as 'n' introduces the parameter, making a fully recursive definition dependent on the input 'n'.
-
Analysis of Term Frequency: We can analyze the frequency of each term. We observe that '1' and 'n' appear twice each, while '2' appears only once. This frequency analysis is particularly relevant if we were to analyze variations or extensions of this sequence.
Expanding the Sequence: Potential Generalizations and Variations
Let's consider variations of this sequence:
-
Adding more elements: We could expand the sequence to include more terms. For example, we might have 1, 2, n, 1, n, m, ... where 'm' represents another variable. This expansion increases the complexity and expands the potential applications.
-
Introducing Operations: We could introduce simple mathematical operations between the terms, such as addition, subtraction, multiplication, or even modular arithmetic (operations performed within a certain range). This opens up a world of possibilities for generating more complex sequences.
-
Using Different Starting Values: Instead of starting with 1 and 2, we could use different starting values, such as a, b, n, a, n, where 'a' and 'b' are variables. This approach introduces further complexity.
Algorithm Design: Generating the Sequence
Creating an algorithm to generate this sequence is straightforward. Here's a Python example:
def generate_sequence(n):
"""Generates the sequence 1, 2, n, 1, n.
Args:
n: The integer value for 'n'.
Returns:
A list representing the sequence.
"""
return [1, 2, n, 1, n]
# Example usage
n_value = 7
sequence = generate_sequence(n_value)
print(f"The sequence for n = {n_value} is: {sequence}")
This code effectively demonstrates how to programmatically generate the sequence for any given value of 'n'. This is a simple example, but more complex algorithms could be developed to handle variations and generalizations of the sequence discussed earlier.
Frequently Asked Questions (FAQ)
-
Q: Is this sequence significant in any established mathematical field? A: Not in a directly established way. It's a relatively simple sequence that doesn't directly align with well-known mathematical patterns or theorems. However, its structure can be used as a foundation for exploring various mathematical concepts and developing more complex sequences.
-
Q: What are the limitations of this sequence? A: Its primary limitation lies in its simplicity. It's a highly specific sequence with limited inherent mathematical complexity. Its applications are mostly conceptual or in simplified models.
-
Q: Can this sequence be used to generate random numbers? A: No, not directly. The sequence is deterministic; given 'n', the sequence is always the same. To generate random numbers, you would need to incorporate additional elements of randomness into the process, such as incorporating a random number generator.
-
Q: What if 'n' is a negative number or a decimal? A: The sequence's definition doesn't inherently exclude negative numbers or decimals. The algorithm would still function; however, the interpretation of the resulting sequence might require a contextual understanding.
Conclusion: A Simple Sequence with Broad Implications
The sequence 1, 2, n, 1, n, though simple, serves as a fertile ground for exploring fundamental concepts in mathematics, computer science, and cryptography. Its apparent simplicity belies its potential for diverse interpretations and applications. By analyzing its structure, considering its variations, and exploring its algorithmic generation, we can appreciate its significance as a starting point for more complex mathematical investigations and practical applications in various fields. Further research focusing on extensions, generalizations, and applications of this basic sequence could lead to exciting new discoveries and insights. The key takeaway is that even the simplest of patterns can hold the seed of profound mathematical and computational exploration.
Latest Posts
Latest Posts
-
Is A Rectangle A Cube
Sep 23, 2025
-
Pka Ph High Vs Low
Sep 23, 2025
-
How To Prove A Rectangle
Sep 23, 2025
-
Gcf Of 18 And 54
Sep 23, 2025
-
Lcm Of 14 And 7
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 2 N 1 N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.