Gcf Of 16 And 4
seoindie
Sep 23, 2025 · 6 min read
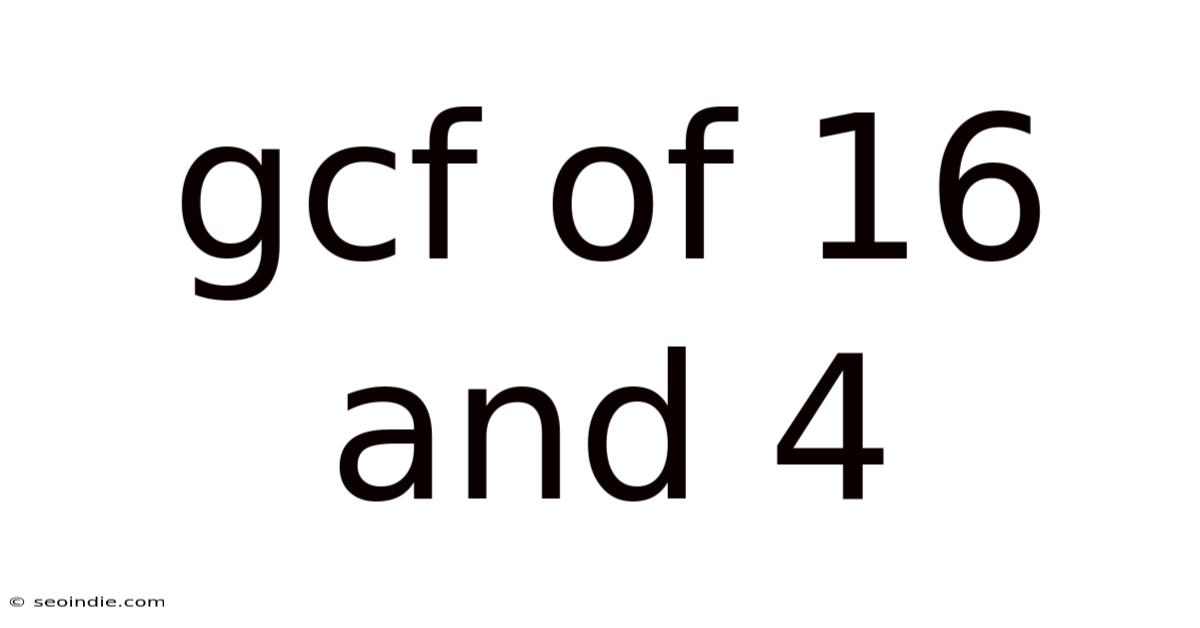
Table of Contents
Finding the Greatest Common Factor (GCF) of 16 and 4: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the highest common factor (HCF) or greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This seemingly simple task lays the groundwork for understanding more complex mathematical operations later on. This article will comprehensively explore how to find the GCF of 16 and 4, using various methods, and will delve deeper into the underlying mathematical principles involved. This guide is perfect for students learning about factors, divisibility, and the GCF, as well as anyone looking to refresh their understanding of these core mathematical concepts.
Understanding Factors and the GCF
Before diving into the calculation, let's clarify some key terms:
-
Factors: Factors are numbers that divide evenly into a given number without leaving a remainder. For example, the factors of 16 are 1, 2, 4, 8, and 16. The factors of 4 are 1, 2, and 4.
-
Greatest Common Factor (GCF): The GCF of two or more numbers is the largest number that divides evenly into all of them. It's the largest factor that they share.
In our case, we want to find the GCF of 16 and 4. This means we need to identify the largest number that is a factor of both 16 and 4.
Method 1: Listing Factors
The simplest method to find the GCF is by listing all the factors of each number and then identifying the largest common factor.
Factors of 16: 1, 2, 4, 8, 16
Factors of 4: 1, 2, 4
Comparing the two lists, we can see that the common factors of 16 and 4 are 1, 2, and 4. The largest of these common factors is 4.
Therefore, the GCF of 16 and 4 is 4.
Method 2: Prime Factorization
Prime factorization is a more powerful method, particularly useful when dealing with larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 16:
16 can be expressed as 2 x 2 x 2 x 2, or 2<sup>4</sup>.
Prime Factorization of 4:
4 can be expressed as 2 x 2, or 2<sup>2</sup>.
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 16 and 4 have the prime factor 2. The lowest power of 2 present in both factorizations is 2<sup>2</sup> (which equals 4).
Therefore, the GCF of 16 and 4 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 16 and 4:
- Start with the larger number (16) and the smaller number (4).
- Divide the larger number by the smaller number and find the remainder: 16 ÷ 4 = 4 with a remainder of 0.
- Since the remainder is 0, the smaller number (4) is the GCF.
Therefore, the GCF of 16 and 4 is 4.
Mathematical Explanation and Significance
The GCF has several significant applications in various mathematical contexts:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For instance, the fraction 16/4 can be simplified by dividing both the numerator and denominator by their GCF (4), resulting in the simplified fraction 4/1 or simply 4.
-
Algebraic Expressions: Finding the GCF is essential when factoring algebraic expressions. This allows for simplification and solving equations more efficiently. For example, consider the expression 16x + 4y. The GCF of 16 and 4 is 4, so the expression can be factored as 4(4x + y).
-
Geometry and Measurement: The GCF is often used in geometry problems involving lengths, areas, and volumes. For example, if you have two rectangular pieces of fabric with dimensions 16cm x 16cm and 4cm x 4cm, finding the GCF helps to determine the largest possible square tiles that can be used to cover both pieces without any wastage.
Real-World Applications of GCF
While seemingly abstract, the concept of the GCF has practical applications in everyday life:
-
Division of items: Imagine you have 16 apples and 4 oranges. You want to distribute these fruits equally among several friends without having any leftovers. The GCF of 16 and 4 (which is 4) tells you that you can share the fruit with a maximum of 4 friends, giving each friend 4 apples and 1 orange.
-
Packaging and organization: Consider a factory producing boxes of 16 candies and another producing boxes of 4 cookies. They want to create larger display boxes containing the same amount of candies and cookies. The GCF of 16 and 4 determines the largest number of sets of candies and cookies that can be packaged together without leaving any leftovers.
-
Time Management and Scheduling: If an activity takes 16 minutes and another takes 4 minutes, the GCF helps determine the shortest repeating cycle or interval where both activities can be performed.
Further Exploration: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 16, 4, and 8:
- Listing Factors: List the factors of each number and identify the largest common factor.
- Prime Factorization: Find the prime factorization of each number and identify the common prime factors with their lowest powers.
- Euclidean Algorithm: The Euclidean algorithm can be applied iteratively to find the GCF of more than two numbers.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they don't share any common factors other than 1.
Q2: Is the GCF always smaller than the numbers involved?
A2: Yes, the GCF will always be less than or equal to the smallest of the numbers involved. It can only be equal to the smallest number if the smallest number is a factor of the larger number.
Q3: Are there any other methods to find the GCF?
A3: Yes, there are other less common methods, such as using Venn diagrams to visually represent the factors and identifying common elements. However, the methods described above are the most efficient and widely used.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with broad applications across various fields. This article has explored three common methods for calculating the GCF – listing factors, prime factorization, and the Euclidean algorithm – providing a comprehensive understanding of the concept and its practical significance. By mastering these methods, you'll not only solve GCF problems effectively but also gain a deeper understanding of number theory and its relevance in both academic and real-world scenarios. Remember, practice is key to mastering any mathematical concept, so try working through different examples to solidify your understanding.
Latest Posts
Latest Posts
-
Is A Rectangle A Cube
Sep 23, 2025
-
Pka Ph High Vs Low
Sep 23, 2025
-
How To Prove A Rectangle
Sep 23, 2025
-
Gcf Of 18 And 54
Sep 23, 2025
-
Lcm Of 14 And 7
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.