X 3 X 5 2
seoindie
Sep 21, 2025 · 6 min read
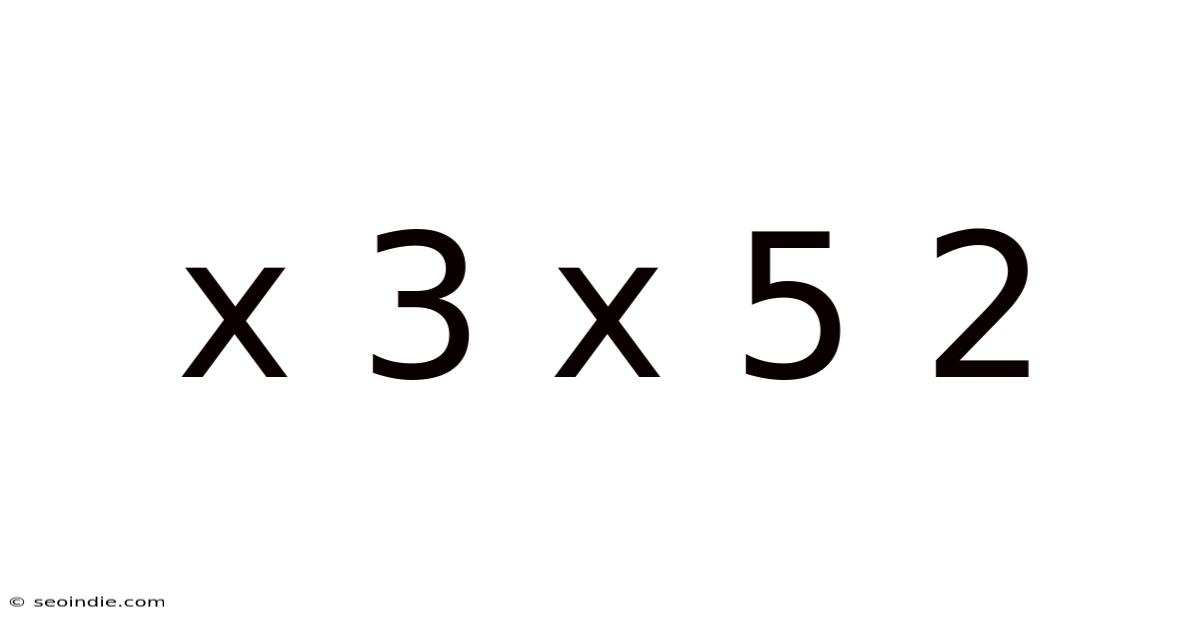
Table of Contents
Decoding the Enigma: A Deep Dive into X³ X⁵ ²
This article explores the mathematical expression "x³ x⁵ ²," breaking down its components, explaining its simplification, and demonstrating its applications in various mathematical contexts. We'll uncover the underlying principles of exponents and powers, clarifying common misconceptions and building a strong understanding of this seemingly simple yet powerful expression. Understanding this expression is key to mastering algebraic manipulation and lays the foundation for more advanced mathematical concepts.
Understanding the Fundamentals: Exponents and Powers
Before delving into the specifics of "x³ x⁵ ²," let's refresh our understanding of exponents and powers. An exponent (or power) indicates how many times a base number is multiplied by itself. For instance:
- x² means x * x (x multiplied by itself twice)
- x³ means x * x * x (x multiplied by itself three times)
- x⁵ means x * x * x * x * x (x multiplied by itself five times)
The number being multiplied is called the base (in these examples, 'x'). The small, raised number is the exponent. Understanding this fundamental concept is crucial for simplifying our expression.
Simplifying x³ x⁵ ²: A Step-by-Step Approach
The expression "x³ x⁵ ²" presents a combination of exponents and powers. To simplify it, we need to apply the rules of exponents. Let's break down the simplification process step-by-step:
Step 1: Addressing the Parentheses
The presence of parentheses around "x⁵" implies that the exponent ² applies to the entire term x⁵. This means we need to square the term x⁵:
(x⁵)² = x⁵ * x⁵
This follows the rule of exponents that states (aᵐ)ⁿ = aᵐⁿ. In our case, a = x, m = 5, and n = 2. Therefore:
(x⁵)² = x⁽⁵*²⁾ = x¹⁰
Step 2: Combining the Terms
Now our expression becomes:
x³ * x¹⁰
This involves multiplying terms with the same base (x). When multiplying terms with the same base, we add the exponents. This is a fundamental rule of exponents stated as aᵐ * aⁿ = aᵐ⁺ⁿ.
Therefore:
x³ * x¹⁰ = x⁽³⁺¹⁰⁾ = x¹³
Step 3: Final Simplified Form
After applying the rules of exponents, the simplified form of the expression "x³ x⁵ ²" is x¹³. This means x multiplied by itself thirteen times.
Expanding the Understanding: Different Perspectives
While the above simplification is straightforward, let's examine alternative approaches to reinforce our understanding and explore different mathematical perspectives.
Approach 1: Expanding the Terms First
We could initially expand each term and then multiply them:
x³ = x * x * x x⁵ = x * x * x * x * x
(x⁵)² = (x * x * x * x * x) * (x * x * x * x * x) = x¹⁰
Then, combining x³ and x¹⁰:
x³ * x¹⁰ = (x * x * x) * (x * x * x * x * x * x * x * x * x * x) = x¹³
This approach demonstrates the fundamental meaning of exponents, providing a visual representation of the multiplication process. However, it becomes less efficient with larger exponents.
Approach 2: Using Logarithmic Properties (Advanced)
For more advanced learners, understanding logarithmic properties can provide an alternative perspective. While not directly used for simplification in this instance, it helps illustrate the interconnectedness of mathematical concepts. We can use logarithmic identities to express the exponents and then manipulate the logarithms before converting back to exponential form. This would involve converting x³ and x¹⁰ into their logarithmic equivalents, applying logarithmic properties (specifically rules related to multiplication), and then converting the result back into exponential form to obtain x¹³ . This method demonstrates a deeper level of understanding of logarithmic relationships with exponential functions.
Illustrative Examples and Practical Applications
Let's consider some examples to illustrate the application of this simplified expression:
Example 1: If x = 2, then x¹³ = 2¹³ = 8192. This demonstrates the practical calculation using the simplified expression.
Example 2: In computer science, this type of expression might represent the number of operations required in a particular algorithm. The exponent (13 in this case) can indicate the complexity of the algorithm, and the base (x) can represent a factor influencing the processing time. Understanding the simplification allows for a more efficient analysis of algorithmic complexity.
Example 3: In physics, similar expressions can model exponential growth or decay. The value of 'x' might represent a constant factor related to a physical phenomenon, while the exponent represents the time or some other variable influencing growth or decay. This simplified expression allows for the prediction of future states of the system.
These examples showcase the practical applicability of simplifying mathematical expressions across multiple disciplines. The ability to efficiently manipulate these expressions leads to more accurate and efficient solutions.
Common Mistakes and Misconceptions
It's essential to address some common mistakes to avoid when working with exponents:
-
Misinterpreting Parentheses: Failing to apply the exponent outside the parentheses correctly is a frequent error. Remember that (x⁵)² means x⁵ multiplied by itself, not simply 2 multiplied by 5.
-
Incorrectly Adding Exponents When Multiplying: A common error is adding exponents when multiplying terms with different bases. For example, x² * y³ cannot be simplified to (xy)⁵. The rule of adding exponents only applies when the bases are the same.
-
Forgetting Order of Operations (PEMDAS/BODMAS): Always adhere to the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) when simplifying complex expressions. Neglecting this can lead to incorrect results.
Frequently Asked Questions (FAQ)
Q: What if the expression was x³ + x⁵ ²?
A: The plus sign indicates addition, not multiplication. In this case, you would simplify (x⁵)² to x¹⁰ first and then add it to x³. The simplified expression would be x³ + x¹⁰, and it cannot be further simplified because the bases are the same, but the exponents are being added, not multiplied.
Q: Can this type of simplification be applied to expressions with different variables?
A: No. The simplification strategy above relies on the rule of adding exponents when multiplying terms with the same base. If the expression involved different variables (e.g., x³y² z⁵), this specific method of simplification wouldn't apply.
Q: What happens if the exponent is negative?
A: A negative exponent means the reciprocal of the positive exponent. For instance, x⁻² = 1/x². The rules of exponents still apply, but the reciprocal must be considered.
Conclusion: Mastering the Fundamentals of Exponents
This comprehensive exploration of "x³ x⁵ ²" has demonstrated the importance of understanding fundamental concepts such as exponents, powers, and the rules governing their manipulation. By breaking down the expression step-by-step, we've not only simplified the expression to its simplest form (x¹³) but also built a solid foundation for tackling more complex mathematical challenges. Remembering the rules of exponents and practicing with various examples will strengthen your ability to simplify expressions and confidently navigate more advanced mathematical concepts. The key takeaways are to understand the meaning of exponents, remember the rules for manipulating them (especially when multiplying terms with the same base), and always carefully follow the order of operations. Mastering these fundamentals is essential for success in algebra and many other mathematical fields.
Latest Posts
Latest Posts
-
Describing Words Start With S
Sep 21, 2025
-
Partes Internas Del Cuerpo Humano
Sep 21, 2025
-
8 Quarts To Cubic Feet
Sep 21, 2025
-
8 X 4 X 2
Sep 21, 2025
-
Difference Between Tree And Plant
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.