8 X 4 X 2
seoindie
Sep 21, 2025 · 5 min read
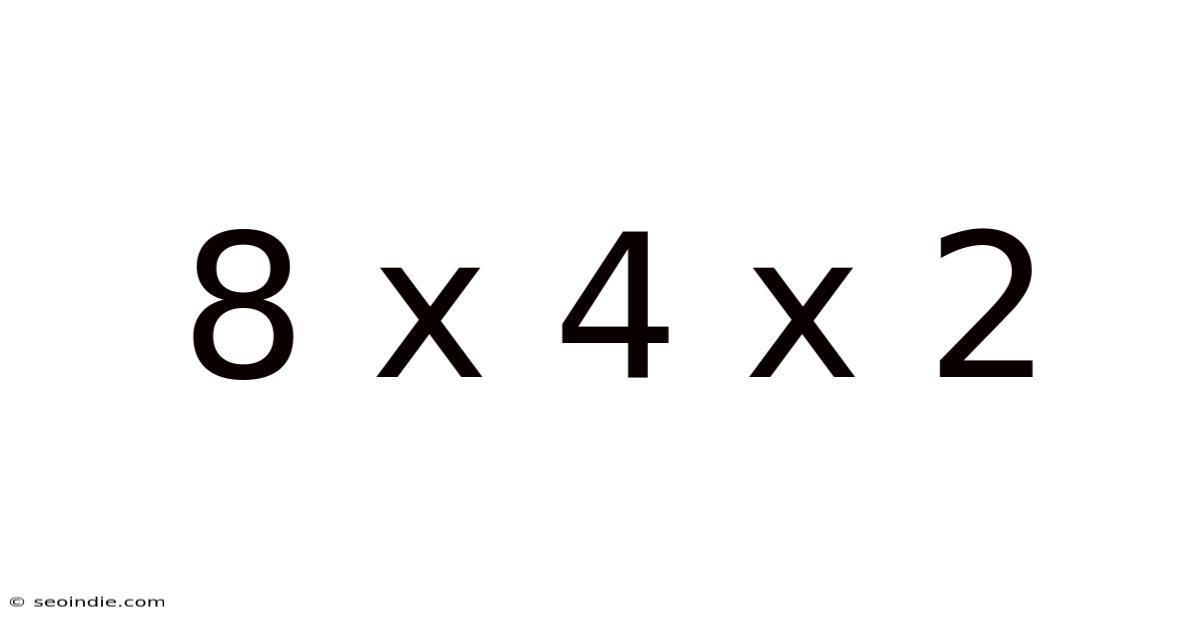
Table of Contents
Decoding 8 x 4 x 2: A Deep Dive into Multiplication, Volume, and Real-World Applications
This article explores the seemingly simple mathematical expression "8 x 4 x 2," delving beyond the basic calculation to uncover its significance in various contexts, including multiplication fundamentals, volume calculations, and its practical applications in everyday life and advanced fields. Understanding this seemingly simple equation provides a solid foundation for more complex mathematical concepts and problem-solving.
Understanding Multiplication: The Foundation of 8 x 4 x 2
At its core, "8 x 4 x 2" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. In this case, we are repeatedly adding the number 8, four times, and then doubling the result. This can be visualized in several ways:
- Repeated Addition: 8 + 8 + 8 + 8 = 32; then 32 + 32 = 64
- Arrays: Imagine an array of objects arranged in a rectangular prism. You have 8 objects in one row, 4 rows in total, and the entire array is duplicated. This creates a 3-dimensional structure.
- Factors and Products: In the equation 8 x 4 x 2 = 64, 8, 4, and 2 are called factors, and 64 is the product. Understanding factors is crucial in various mathematical concepts like factoring and prime factorization.
The order in which you multiply the numbers doesn't change the final product; this is known as the commutative property of multiplication. For example, 8 x 4 x 2 = 8 x 2 x 4 = 4 x 8 x 2 = 64. This property is incredibly useful for simplifying calculations.
Calculating Volume: A Three-Dimensional Perspective
The equation 8 x 4 x 2 takes on a particularly significant meaning when considering volume. Volume refers to the amount of space occupied by a three-dimensional object. If we imagine a rectangular prism (like a box), the equation directly relates to its dimensions:
- Length: 8 units
- Width: 4 units
- Height: 2 units
Therefore, 8 x 4 x 2 represents the volume of this rectangular prism. The result, 64, signifies the number of cubic units that the box can hold. This could be cubic centimeters, cubic meters, cubic inches, or any other cubic unit, depending on the context.
Understanding volume calculations is critical in numerous real-world applications. From calculating the amount of concrete needed for a foundation to determining the capacity of a storage container, the ability to calculate volume is indispensable.
Real-World Applications: Beyond the Classroom
The seemingly simple calculation of 8 x 4 x 2 finds its way into a wide range of practical applications across various disciplines:
-
Construction and Engineering: As mentioned earlier, calculating the volume of materials is crucial for construction projects. This extends beyond simple boxes to more complex structures, requiring a nuanced understanding of volume calculations. Engineers use similar principles to design structures, calculate material requirements, and ensure structural integrity.
-
Packaging and Logistics: Companies involved in packaging and shipping rely heavily on volume calculations. Efficient packaging minimizes wasted space and shipping costs. Determining the optimal size and shape of packages to maximize capacity and minimize material usage is critical for profitability.
-
Agriculture and Farming: Farmers use volume calculations to determine the amount of fertilizer, pesticides, or water required for their crops. Understanding volume helps optimize resource allocation and improve yields.
-
Medicine and Healthcare: Volume calculations play a vital role in various medical procedures, such as calculating dosages of medication or determining the volume of fluids needed during surgery. Precision in volume measurement is crucial for patient safety and effective treatment.
-
Data Analysis and Computing: While less obvious, volume calculations can be extended to data analysis and computing. Consider the concept of data storage. The amount of data that can be stored on a hard drive or in a cloud server is directly related to its storage capacity, which can be viewed as a volume of data.
-
Manufacturing and Production: Manufacturers use volume calculations to design molds, determine material requirements, and optimize production processes. Understanding volume is essential for streamlining production and minimizing waste.
Expanding the Concept: Beyond Simple Multiplication
The equation 8 x 4 x 2 provides a springboard to explore more complex mathematical concepts:
-
Exponents: The repeated multiplication can be expressed using exponents. For instance, 2³ (2 cubed) means 2 x 2 x 2 = 8. This shows how repeated multiplication forms the basis of exponents.
-
Algebra: Introducing variables into the equation allows for more general solutions. For example, let's say the length of a box is 'x', the width is 'y', and the height is 'z'. The volume would be represented as V = xyz. This simple algebraic representation can be used to solve for any of the variables if the other two are known.
Frequently Asked Questions (FAQ)
-
What is the simplest way to calculate 8 x 4 x 2? The simplest approach is to multiply the numbers in any order. For example, (8 x 4) x 2 = 32 x 2 = 64, or 8 x (4 x 2) = 8 x 8 = 64.
-
Can I use a calculator to solve this? Absolutely! Calculators are valuable tools for solving multiplication problems, especially those involving larger numbers.
-
What if the numbers were different? The same principles apply regardless of the numbers used. The equation still represents a volume calculation if the numbers represent the dimensions of a rectangular prism.
-
How important is understanding the order of operations (PEMDAS/BODMAS)? While the commutative property of multiplication makes order less critical in this specific example, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) becomes crucial when dealing with more complex equations containing different arithmetic operations.
Conclusion: The Power of a Simple Equation
The seemingly simple equation 8 x 4 x 2 offers a valuable gateway to understanding fundamental mathematical concepts, including multiplication, volume calculations, and their wide-ranging real-world applications. From constructing buildings to packaging products and analyzing data, the ability to perform these calculations is a crucial skill across numerous fields. By appreciating the versatility and significance of this basic equation, we gain a deeper understanding of the power and utility of mathematics in our daily lives. Its simplicity belies the vast implications it holds for problem-solving and innovation in various disciplines. The exploration of this seemingly simple calculation underscores the importance of building a strong foundation in mathematics – a foundation that supports countless advanced concepts and real-world endeavors.
Latest Posts
Latest Posts
-
How Tall Is 11 Cm
Sep 22, 2025
-
What Is Equivalent To 1 4
Sep 22, 2025
-
3 Functions Of A Protein
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.