What Times What Equals 196
seoindie
Sep 17, 2025 · 5 min read
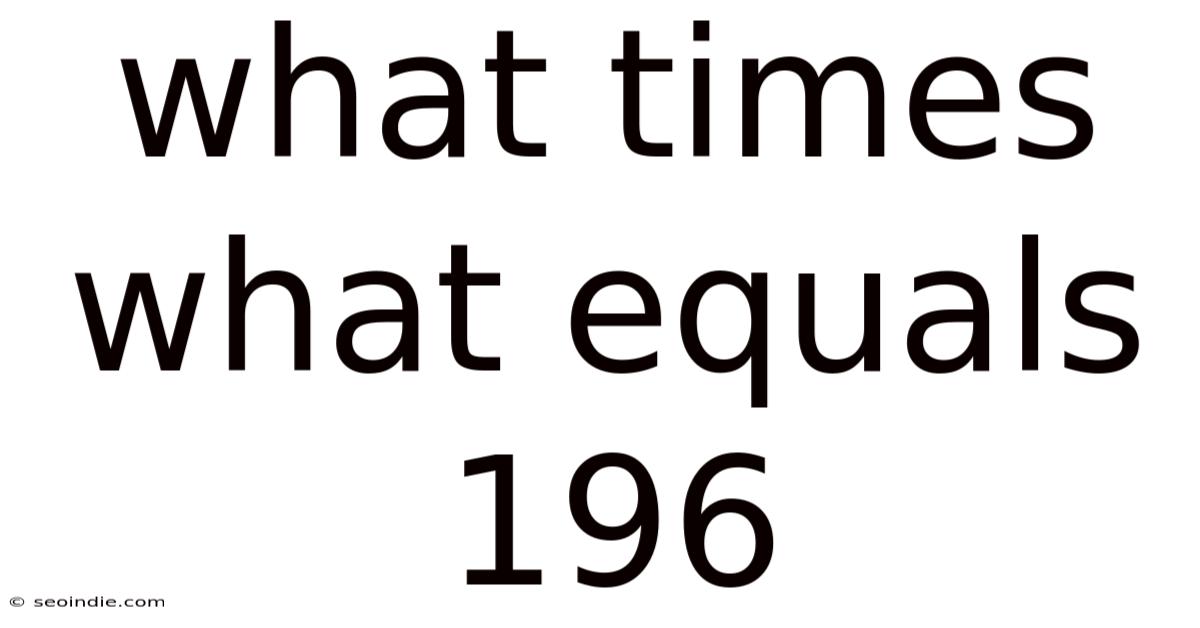
Table of Contents
What Times What Equals 196? A Deep Dive into Factorization and Number Theory
Finding the factors of a number, like solving "what times what equals 196?", might seem like a simple arithmetic problem. However, this seemingly basic question opens the door to a fascinating world of number theory, factorization, and even practical applications in cryptography and computer science. This article will explore various methods to solve this problem and delve deeper into the underlying mathematical concepts.
Introduction: Understanding Factor Pairs
The question "what times what equals 196?" is essentially asking us to find the factor pairs of 196. A factor pair consists of two numbers that, when multiplied together, result in the given number (in this case, 196). We can start by systematically searching for these pairs. Let's begin with the most obvious factors:
- 1 and 196: 1 x 196 = 196
- 2 and 98: 2 x 98 = 196
We can continue this process, testing small whole numbers. However, this method can become inefficient for larger numbers. Therefore, we need more sophisticated approaches to discover all the factor pairs effectively.
Method 1: Prime Factorization – The Building Blocks of Numbers
Prime factorization is a fundamental concept in number theory. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). Every composite number (a number that is not prime) can be expressed as a unique product of prime numbers. This unique product is called its prime factorization.
Let's find the prime factorization of 196:
- Divide 196 by the smallest prime number, 2: 196 ÷ 2 = 98
- Divide 98 by 2: 98 ÷ 2 = 49
- Now, 49 is not divisible by 2, 3, or 5. However, it is divisible by 7: 49 ÷ 7 = 7
- 7 is a prime number.
Therefore, the prime factorization of 196 is 2 x 2 x 7 x 7, or 2² x 7².
Knowing the prime factorization allows us to easily find all factor pairs. We can combine the prime factors in different ways:
- 2 x 98
- 4 x 49
- 7 x 28
- 14 x 14
This method is much more systematic and efficient than randomly trying different numbers, especially for larger numbers.
Method 2: Using Division and Observation
We can also systematically test divisors by dividing 196 by consecutive whole numbers, starting from 1 and going up until the quotient becomes smaller than the divisor. This method will reveal all factor pairs.
- 196 ÷ 1 = 196 (1, 196)
- 196 ÷ 2 = 98 (2, 98)
- 196 ÷ 4 = 49 (4, 49)
- 196 ÷ 7 = 28 (7, 28)
- 196 ÷ 14 = 14 (14, 14)
At this point, we've found all factor pairs because the next divisor would be 14, and we've already found the (14,14) pair. This shows us that 14 is the square root of 196, an important point we'll discuss further below.
Method 3: Utilizing the Square Root – A Shortcut
For finding factors, the square root of the number is a crucial point. If a number has an integer square root, it indicates that the number is a perfect square and has a factor pair where both numbers are identical.
The square root of 196 is 14 (14 x 14 = 196). This tells us immediately that 14 is a factor, and consequently, (14, 14) is a factor pair. Any factor pair where one number is smaller than 14 will have a corresponding pair where the other number is larger than 14. This provides a significant shortcut in our search.
Understanding the Significance of Factorization
The ability to find the factors of a number is not merely a mathematical exercise; it has many important applications:
-
Cryptography: Factorization is a cornerstone of many modern encryption techniques. The difficulty in factoring very large numbers into their prime components is what ensures the security of data transmitted over the internet.
-
Computer Science: Algorithms for factorization are used in various computational tasks, including optimization and database management.
-
Number Theory: Factorization is a central concept in number theory, contributing to our understanding of prime numbers, divisibility, and related mathematical structures.
-
Algebra: Factorization is essential for simplifying algebraic expressions and solving equations.
Frequently Asked Questions (FAQ)
-
Q: Is there only one answer to "what times what equals 196?"
- A: No, there are several factor pairs that satisfy this equation, as we have demonstrated above.
-
Q: How can I find factors of larger numbers quickly?
- A: For larger numbers, using prime factorization or sophisticated algorithms is much more efficient than manual trial and error. Computational tools and software can greatly assist in this process.
-
Q: What if the number isn't a perfect square?
- A: If the number is not a perfect square, it will still have factor pairs, but none of them will have two identical numbers. The process of prime factorization remains the most reliable method for finding all factor pairs.
-
Q: Are negative numbers considered when finding factors?
- A: Yes, if we're considering all possible solutions, we would also include negative factor pairs, such as (-1, -196), (-2, -98), etc. However, the question usually implies positive integer factors.
Conclusion: Beyond the Simple Calculation
Solving the seemingly simple problem of "what times what equals 196?" leads us to explore the rich and fascinating world of number theory and its practical applications. While the basic solution can be found through trial and error, understanding prime factorization and using the square root as a shortcut provides far more efficient and elegant methods. This ability to decompose numbers into their fundamental building blocks – their prime factors – underlies many critical aspects of mathematics and computer science. So, the next time you encounter a factorization problem, remember that it's more than just a calculation; it’s a gateway to a deeper understanding of mathematical structures and their power in our world. The ability to effectively find factors of a number is a skill that extends far beyond simple arithmetic, demonstrating the interconnectedness of seemingly unrelated mathematical concepts. Mastering this skill not only enhances your mathematical proficiency but also opens doors to more advanced mathematical explorations and applications.
Latest Posts
Latest Posts
-
Escape Speed From Earth Is
Sep 17, 2025
-
Gcf Of 49 And 56
Sep 17, 2025
-
All The Multiples Of 18
Sep 17, 2025
-
Centroid Of A Triangle Calculator
Sep 17, 2025
-
Lcm Of 15 And 24
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 196 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.