Gcf Of 49 And 56
seoindie
Sep 17, 2025 · 7 min read
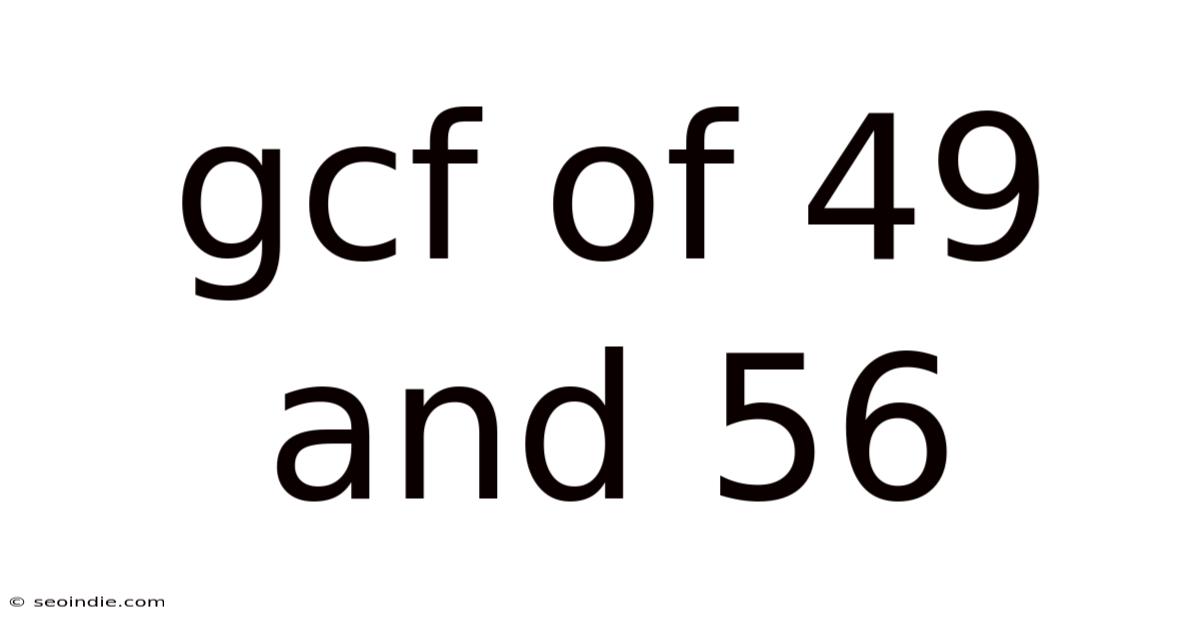
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 49 and 56: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and different methods for calculating the GCF provides a valuable foundation in number theory, with applications extending far beyond basic arithmetic. This article will explore the GCF of 49 and 56 in detail, demonstrating multiple approaches and illuminating the broader mathematical concepts involved. We'll delve into the prime factorization method, the Euclidean algorithm, and even consider the application of these concepts to more complex scenarios.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding the GCF is crucial in various mathematical operations, including simplifying fractions, solving equations, and working with modular arithmetic. For example, finding the GCF of 49 and 56 allows us to simplify the fraction 49/56 to its simplest form.
Method 1: Prime Factorization
The prime factorization method is a fundamental approach to determining the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this method to find the GCF of 49 and 56:
- Prime factorization of 49: 49 = 7 x 7 = 7²
- Prime factorization of 56: 56 = 2 x 2 x 2 x 7 = 2³ x 7
Now, we identify the common prime factors and their lowest powers. Both 49 and 56 share the prime factor 7, but 49 has 7 to the power of 2, and 56 only has 7 to the power of 1. Therefore, the lowest power of 7 is 7¹.
Therefore, the GCF of 49 and 56 is 7.
This method is intuitive and provides a clear understanding of the underlying structure of the numbers. However, for larger numbers, finding the prime factorization can become computationally intensive.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 49 and 56:
- Start with the larger number (56) and the smaller number (49): 56 and 49.
- Subtract the smaller number from the larger number: 56 - 49 = 7.
- Replace the larger number with the result (7), and keep the smaller number (49): 7 and 49.
- Repeat the subtraction: 49 - 7 = 42.
- Repeat: 42 - 7 = 35.
- Repeat: 35 - 7 = 28.
- Repeat: 28 - 7 = 21.
- Repeat: 21 - 7 = 14.
- Repeat: 14 - 7 = 7.
- The result is 7, which is the GCF. The process stops when the result of the subtraction is 7, which means that 7 divides both 49 and 56 completely.
A more efficient version of the Euclidean algorithm uses division instead of repeated subtraction. We divide the larger number by the smaller number and take the remainder. Then, we replace the larger number with the smaller number and the smaller number with the remainder. We repeat this process until the remainder is 0. The last non-zero remainder is the GCF.
Let's illustrate this using 49 and 56:
- Divide 56 by 49: 56 = 49 x 1 + 7 (Remainder = 7)
- Divide 49 by 7: 49 = 7 x 7 + 0 (Remainder = 0)
The last non-zero remainder is 7, confirming that the GCF of 49 and 56 is 7. This method is significantly faster than repeated subtraction, especially for larger numbers.
Method 3: Listing Factors
A simpler, albeit less efficient for larger numbers, method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 49: 1, 7, 49
- Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
By comparing the lists, we see that the largest common factor is 7. This method is straightforward for smaller numbers but becomes cumbersome and time-consuming for larger integers.
The Significance of the GCF: Applications Beyond Simple Arithmetic
The GCF has far-reaching applications in various mathematical fields and practical scenarios:
- Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 49/56 can be simplified to 7/8 by dividing both the numerator and denominator by their GCF (7).
- Least Common Multiple (LCM): The GCF is closely related to the least common multiple (LCM). The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. This relationship is useful in solving problems involving fractions and ratios. Knowing the GCF helps determine the LCM more efficiently.
- Algebra and Equation Solving: The GCF plays a role in factoring polynomials and simplifying algebraic expressions. Finding the GCF of the terms in a polynomial allows for factorization, simplifying the expression and making it easier to solve equations.
- Cryptography: Number theory, including concepts like the GCF, forms the basis of many cryptographic algorithms used for secure communication and data protection.
- Computer Science: Efficient algorithms for finding the GCF, like the Euclidean algorithm, are fundamental in computer science applications involving number theory and cryptography.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, we simply find the prime factorization of each number and identify the common prime factors with the lowest powers. For the Euclidean algorithm, we can iteratively find the GCF of pairs of numbers. For example, to find the GCF of 28, 42, and 56:
- Find the GCF of 28 and 42 (using the Euclidean Algorithm or prime factorization): GCF(28, 42) = 14
- Find the GCF of the result (14) and the remaining number (56): GCF(14, 56) = 14
Therefore, the GCF of 28, 42, and 56 is 14.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the GCF of two numbers be greater than the smaller number?
- A: No, the GCF can never be greater than the smaller of the two numbers.
-
Q: Is there a limit to the size of numbers for which the GCF can be calculated?
- A: Theoretically, there's no limit. However, the computational time for methods like prime factorization can increase significantly with very large numbers. The Euclidean algorithm remains highly efficient even for very large numbers.
-
Q: Why is the Euclidean algorithm more efficient than the prime factorization method for large numbers?
- A: The Euclidean algorithm's efficiency stems from its iterative approach, avoiding the need to find the complete prime factorization of the numbers. Finding prime factors for very large numbers can be computationally expensive, whereas the Euclidean algorithm's steps are relatively simple and quick, even for large inputs.
Conclusion: Mastering the GCF
Understanding the greatest common factor is not just about performing a simple calculation; it's about grasping fundamental concepts in number theory that have broad applications in mathematics and computer science. This article has explored multiple methods for determining the GCF, focusing on the prime factorization and Euclidean algorithm methods, highlighting their strengths and weaknesses. By mastering these techniques, you gain valuable skills for simplifying fractions, solving equations, and appreciating the deeper mathematical structures underlying seemingly simple arithmetic operations. The seemingly simple task of finding the GCF of 49 and 56 opens the door to a fascinating world of mathematical exploration. Remember, practice is key to mastering these concepts, so try applying these methods to different pairs of numbers to solidify your understanding.
Latest Posts
Latest Posts
-
Lcm Of 7 5 6
Sep 17, 2025
-
What Percent Is One Third
Sep 17, 2025
-
Difference Between Capability And Ability
Sep 17, 2025
-
Difference Between Geometry And Trigonometry
Sep 17, 2025
-
Mass Moment Of Inertia Disc
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 49 And 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.