What Percent Is 3 8
seoindie
Sep 22, 2025 · 6 min read
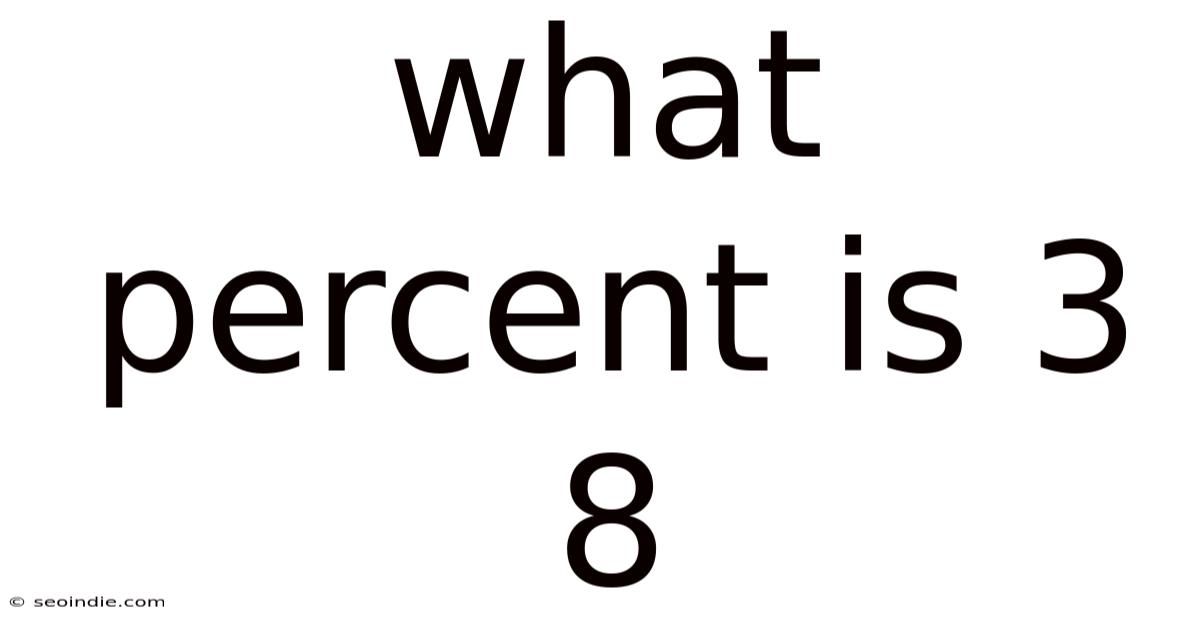
Table of Contents
What Percent is 3/8? Understanding Fractions, Decimals, and Percentages
This article will comprehensively explore how to calculate what percentage 3/8 represents, providing a clear understanding of the underlying mathematical principles and offering practical applications. We'll move beyond simply providing the answer to delve into the fundamental concepts of fractions, decimals, and percentages, equipping you with the skills to solve similar problems independently. This will be particularly useful for students learning about ratios, proportions, and percentages, as well as anyone needing to convert between these different representations of numbers in daily life.
Introduction: Fractions, Decimals, and Percentages – A Unified Concept
Before we tackle the specific problem of converting 3/8 to a percentage, let's clarify the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, 3/8 means 3 parts out of a total of 8 equal parts.
-
Decimals: A decimal represents a part of a whole using the base-10 system. The decimal point separates the whole number part from the fractional part. For instance, 0.5 represents one-half (1/2).
-
Percentages: A percentage represents a part of a whole as a fraction of 100. The symbol "%" signifies "per hundred." So, 50% means 50 out of 100, or 50/100, which is equivalent to 1/2 or 0.5.
These three forms are interchangeable; you can convert between them using simple mathematical operations. Understanding this interchangeability is crucial for solving problems involving proportions and ratios.
Method 1: Direct Conversion from Fraction to Percentage
The most straightforward way to determine what percentage 3/8 represents is to convert the fraction into a decimal and then into a percentage.
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
3 ÷ 8 = 0.375
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.375 x 100 = 37.5%
Therefore, 3/8 is equal to 37.5%.
Method 2: Using Proportions
Another approach involves setting up a proportion. We know that a percentage is a fraction out of 100. We can set up the following proportion:
3/8 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
8x = 300
Now, divide both sides by 8:
x = 300 ÷ 8 = 37.5
Therefore, x = 37.5%, confirming our previous result. This method highlights the proportional relationship between fractions and percentages.
Method 3: Understanding the Concept of Percentage Increase/Decrease
While the previous methods directly address the conversion, let's also consider how this relates to percentage increase or decrease. Imagine you have a quantity of 8 units, and you gain 3 units. The percentage increase is calculated as follows:
(Increase / Original Amount) x 100% = Percentage Increase
(3 / 8) x 100% = 37.5%
This shows that the increase of 3 units represents a 37.5% increase over the original 8 units. This method is useful when dealing with scenarios involving changes in quantities.
Further Exploration: Working with Percentages in Real-World Applications
Understanding percentage calculations is vital in numerous real-world situations. Here are some examples:
-
Calculating discounts: If an item is discounted by 37.5%, you can easily calculate the final price by subtracting 37.5% of the original price.
-
Determining sales tax: Similarly, you can calculate the sales tax by finding 37.5% of the price and adding it to the original price.
-
Understanding financial reports: Financial statements often use percentages to represent various financial ratios and metrics, such as profit margins or debt-to-equity ratios.
-
Interpreting survey results: Percentages are frequently used to present the results of surveys and polls.
Elaboration on Fraction to Decimal Conversion
The conversion of a fraction to a decimal often involves long division, especially when the denominator is not a factor of 10, 100, 1000, etc. Let's break down the process of converting 3/8 to a decimal step-by-step:
-
Set up the long division: Place the numerator (3) inside the division symbol and the denominator (8) outside.
-
Add a decimal point and zeros: Add a decimal point after the 3 and add zeros as needed. This allows you to continue the division until you reach a remainder of 0 or a repeating pattern.
-
Perform the division: Begin dividing 8 into 3.000...
- 8 does not go into 3, so place a 0 above the decimal point.
- 8 goes into 30 three times (3 x 8 = 24). Place a 3 above the first 0.
- Subtract 24 from 30, leaving a remainder of 6.
- Bring down the next 0.
- 8 goes into 60 seven times (7 x 8 = 56). Place a 7 above the second 0.
- Subtract 56 from 60, leaving a remainder of 4.
- Bring down the next 0.
- 8 goes into 40 five times (5 x 8 = 40). Place a 5 above the third 0.
- The remainder is 0.
The result of the division is 0.375. This demonstrates the process involved in converting fractions, even those that don't readily convert to a simple decimal.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage by following the steps outlined above: divide the numerator by the denominator to get a decimal, then multiply by 100 and add the % sign.
Q: What if the decimal has repeating digits?
A: If the decimal has repeating digits (e.g., 1/3 = 0.333...), you can round the decimal to a certain number of decimal places before converting it to a percentage. For example, 0.333... can be rounded to 0.33 and then converted to 33%. You should always indicate that you have rounded the value.
Q: Are there other ways to calculate percentages?
A: Yes, there are various methods, including using calculators with percentage functions or spreadsheet software. These tools can simplify the calculations, especially for more complex problems.
Q: Why is understanding percentages important?
A: Percentages are essential for understanding and interpreting data across many fields, including finance, statistics, science, and everyday life. They provide a standardized way to compare different quantities and proportions.
Conclusion: Mastering Percentage Calculations
This article has explored the calculation of "What percent is 3/8?" in detail, going beyond a simple answer to provide a comprehensive understanding of the underlying mathematical concepts. We've examined different methods of conversion, highlighted the importance of fractions, decimals, and percentages, and discussed their practical applications. By understanding these concepts and practicing the methods, you will develop confidence in tackling similar problems and enhancing your mathematical skills. Remember that the ability to convert between fractions, decimals, and percentages is a fundamental skill with wide-ranging applications in various aspects of life and work.
Latest Posts
Latest Posts
-
All The Factors Of 85
Sep 22, 2025
-
5 Square Root Of 2
Sep 22, 2025
-
Words That Start With Tac
Sep 22, 2025
-
Words That Start With On
Sep 22, 2025
-
Fruit That Starts With Ac
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.