5 Square Root Of 2
seoindie
Sep 22, 2025 · 5 min read
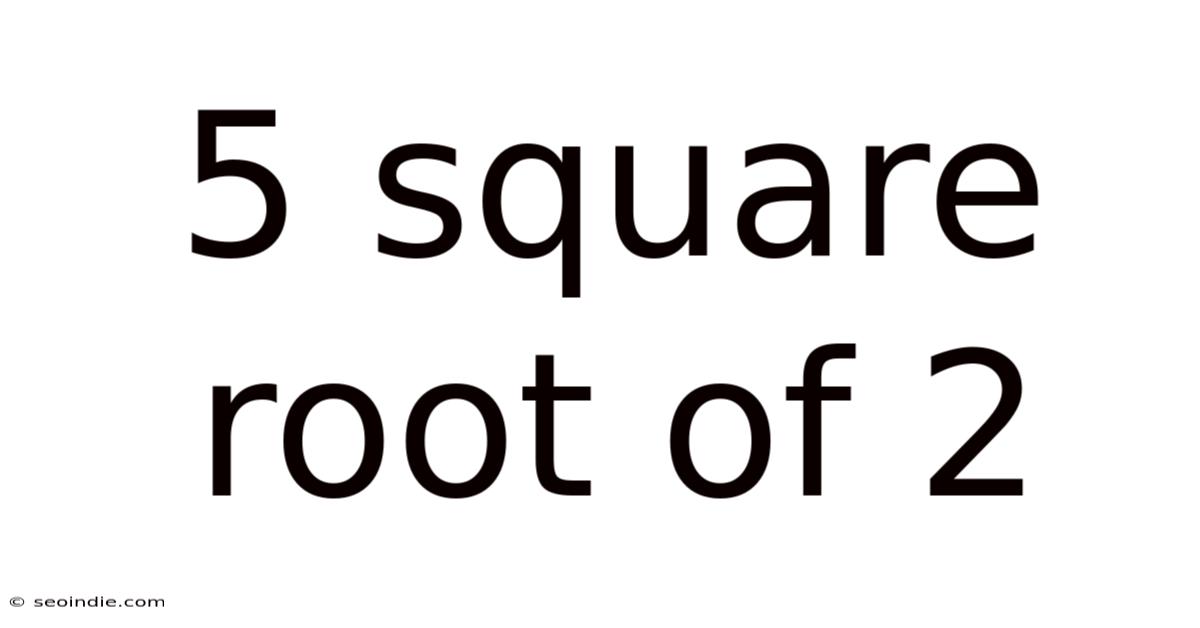
Table of Contents
Decoding the Enigma: Exploring 5√2
The expression "5√2" might seem simple at first glance, a mere combination of a whole number and a square root. However, beneath its unassuming exterior lies a rich tapestry of mathematical concepts, applications, and intriguing properties. This comprehensive exploration delves into the intricacies of 5√2, examining its value, significance in various fields, and the broader mathematical principles it represents. Understanding 5√2 provides a deeper appreciation for the elegance and power of mathematics.
Understanding the Basics: What is 5√2?
At its core, 5√2 represents the product of 5 and the square root of 2. The square root of 2 (√2) is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating, approximately equal to 1.41421356… Therefore, 5√2 is also an irrational number, approximately equal to 7.07106781…
This seemingly simple expression has far-reaching implications in geometry, trigonometry, and various applications within engineering and physics. Let's delve deeper into its properties and significance.
Calculating the Value of 5√2:
While we know 5√2 is irrational, we can approximate its value using various methods. The simplest approach involves multiplying 5 by the approximate value of √2:
5 * 1.41421356… ≈ 7.07106781…
More sophisticated methods, such as using a calculator or computer programming languages, can provide a higher degree of accuracy. However, it's crucial to remember that any decimal representation will only be an approximation, as the true value of √2 (and therefore 5√2) extends infinitely without repetition.
Geometric Interpretations: 5√2 in the World of Shapes
The square root of 2 has a profound geometric connection. It represents the length of the diagonal of a square with sides of length 1. This relationship stems directly from the Pythagorean theorem (a² + b² = c²), where 'a' and 'b' are the sides of a right-angled triangle and 'c' is the hypotenuse. In a square with sides of length 1, the diagonal forms a right-angled triangle with sides of length 1 and 1, meaning the diagonal (c) has a length of √(1² + 1²) = √2.
Scaling this up, 5√2 can represent the diagonal of a square with sides of length 5. Imagine a square with 5-unit sides. Its diagonal would measure 5√2 units. This geometric interpretation underscores the practical relevance of 5√2 in various fields requiring calculations involving angles, distances, and shapes.
Trigonometric Applications: Angles and 5√2
Trigonometric functions, such as sine, cosine, and tangent, are deeply intertwined with the concept of right-angled triangles and their side ratios. The value 5√2 often appears in trigonometric calculations involving angles of 45 degrees.
For example, in a right-angled isosceles triangle (a triangle with two equal sides and a 90-degree angle), the ratio of the hypotenuse to one of the equal sides is √2. If we scale this triangle up by a factor of 5, the hypotenuse would become 5√2. This makes 5√2 relevant in calculations involving vectors, forces, and displacements in physics and engineering.
Applications in Engineering and Physics:
The value 5√2, and more broadly the concept of √2, finds numerous applications in engineering and physics.
-
Civil Engineering: Calculations involving diagonal bracing in structures, stress analysis, and determining optimal dimensions for load-bearing components often involve √2. Imagine designing a bridge; understanding the diagonal forces and their relationship to the supporting structures is crucial, and these calculations often involve numbers like 5√2.
-
Electrical Engineering: In AC circuits, the relationship between voltage, current, and impedance involves phase angles, leading to calculations involving trigonometric functions and frequently incorporating √2.
-
Physics: In mechanics, vectors representing forces or velocities might have components that involve √2, leading to calculations involving 5√2 or similar expressions when scaling these vectors.
Approximations and Error Analysis:
It's crucial to understand that when using approximations of irrational numbers like 5√2, there is inherent error. The degree of accuracy required depends on the application. In some cases, a simple approximation might suffice, while in others, high precision is essential. Understanding error analysis is vital for ensuring the reliability and accuracy of calculations involving 5√2.
Beyond the Basics: Expanding the Understanding
The exploration of 5√2 extends beyond its direct applications. It provides a gateway to a deeper understanding of several key mathematical concepts:
-
Irrational Numbers: The very nature of 5√2 as an irrational number highlights the richness and complexity of the number system. Understanding irrational numbers is essential for grasping the intricacies of calculus, analysis, and advanced mathematical fields.
-
Pythagorean Theorem: The geometric interpretation of 5√2 is directly tied to the Pythagorean theorem, a fundamental principle in geometry and trigonometry with far-reaching consequences.
-
Trigonometry: The appearance of 5√2 in trigonometric calculations underscores the power and utility of trigonometry in modeling real-world phenomena.
Frequently Asked Questions (FAQ):
-
Q: Can 5√2 be simplified further? A: No, 5√2 is already in its simplest form. The 5 is a rational number, and √2 is an irrational number in its simplest form. They cannot be combined further.
-
Q: What is the exact value of 5√2? A: There is no exact decimal representation for 5√2. It is an irrational number, meaning its decimal expansion is infinite and non-repeating.
-
Q: How do I calculate 5√2 without a calculator? A: You can approximate the value by multiplying 5 by an approximation of √2, such as 1.414. However, this will only provide an approximate value. More advanced methods, such as iterative algorithms, can be used for greater accuracy without a calculator but require a deeper mathematical understanding.
Conclusion:
5√2, although seemingly a simple expression, embodies a wealth of mathematical principles and practical applications. Its connection to the square root of 2, the Pythagorean theorem, and trigonometric functions highlights its significance in various fields. Understanding its properties, calculating its value (or approximation), and appreciating its geometric and trigonometric interpretations provide a deeper insight into the fascinating world of mathematics and its relevance to our everyday lives. From the structural integrity of buildings to the intricacies of electrical circuits, the seemingly simple 5√2 plays a significant, often unseen, role in shaping our world. Its exploration encourages a more profound appreciation for the elegance and power inherent within mathematics.
Latest Posts
Latest Posts
-
Density Of A Sphere Formula
Sep 22, 2025
-
Gcf Of 21 And 28
Sep 22, 2025
-
35 Acre To Sq Ft
Sep 22, 2025
-
Adjectives With The Letter D
Sep 22, 2025
-
Steps Of Dna Recombinant Technology
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.