What Is 6 Times 4
seoindie
Sep 22, 2025 · 6 min read
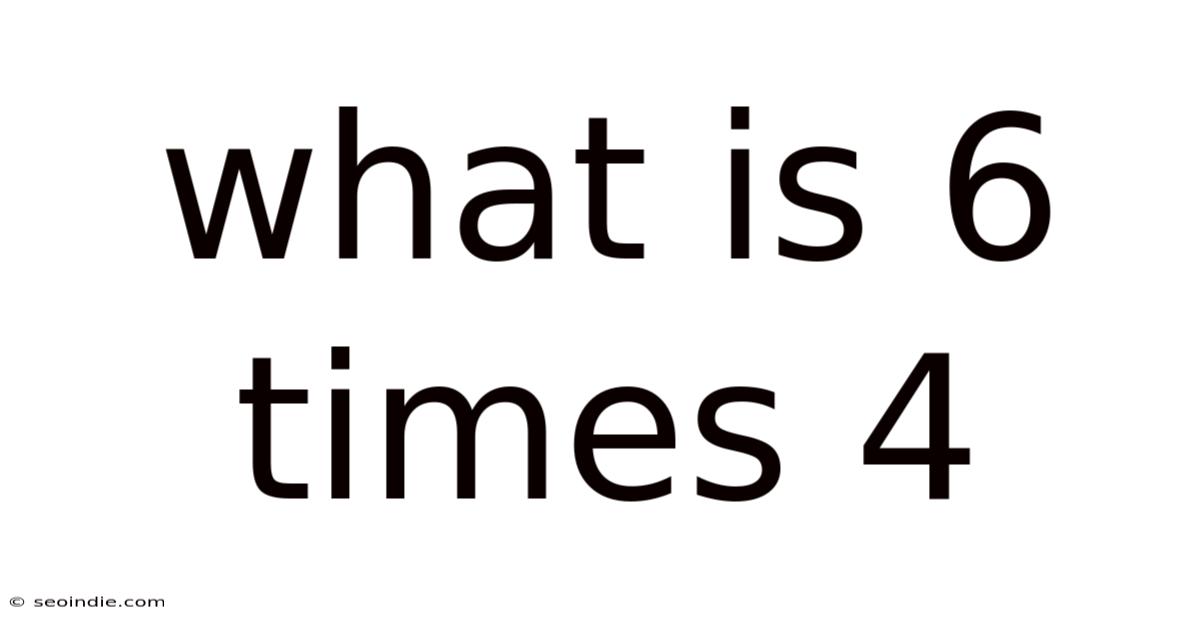
Table of Contents
What is 6 Times 4? A Deep Dive into Multiplication
What is 6 times 4? This seemingly simple question opens the door to a fascinating exploration of multiplication, a fundamental concept in mathematics that underpins countless aspects of our daily lives. This article will not only answer the question directly but also delve into the underlying principles, different approaches to solving the problem, and its broader applications. We'll explore the concept of multiplication itself, examine different methods for calculating 6 x 4, and discuss the significance of this basic arithmetic operation in more advanced mathematical contexts.
Understanding Multiplication: Beyond Simple Repetition
At its core, multiplication is repeated addition. When we say "6 times 4," we're essentially asking: what is the sum of six fours? This can be represented visually:
- 4 + 4 + 4 + 4 + 4 + 4 = 24
This simple equation clearly demonstrates that 6 times 4 equals 24. However, understanding multiplication goes beyond simply adding numbers repeatedly. It represents a fundamental relationship between quantities, providing a concise way to express repeated addition and scale calculations efficiently.
Different Methods for Calculating 6 x 4
While the repeated addition method is straightforward, several other approaches can be used to calculate 6 x 4. These methods not only provide alternative solutions but also enhance our understanding of multiplication's underlying principles:
-
Using a Multiplication Table: The most common method involves using a multiplication table, a fundamental tool in elementary mathematics. Locating the intersection of the '6' row and the '4' column will directly provide the answer: 24. This method relies on memorization, making it efficient for quick calculations.
-
Skip Counting: Another effective technique is skip counting. Starting at 0, count by fours six times: 4, 8, 12, 16, 20, 24. This method reinforces the connection between multiplication and repeated addition, offering a more hands-on approach.
-
Array Method: Visual learners benefit greatly from the array method. Imagine a rectangular array with six rows and four columns. By counting the total number of squares in the array (6 x 4 = 24), we arrive at the answer. This method visually represents the concept of multiplication as area calculation, a vital concept in geometry.
-
Distributive Property: This method involves breaking down the problem into smaller, easier-to-manage parts. For example, we can represent 6 x 4 as (5 x 4) + (1 x 4). Since 5 x 4 = 20 and 1 x 4 = 4, we can simply add these results: 20 + 4 = 24. This approach introduces the distributive property, a fundamental concept in algebra.
-
Using a Calculator: In today's digital age, calculators provide a rapid and convenient way to calculate multiplication problems. Entering '6 x 4' into a calculator immediately yields the answer: 24. While this method lacks the educational value of the previous methods, it's efficient for quick calculations, especially with larger numbers.
The Significance of 6 x 4 in Mathematics and Beyond
The simple equation "6 x 4 = 24" is more than just a basic arithmetic calculation; it forms the bedrock for more complex mathematical concepts and real-world applications:
-
Foundation for Algebra: Understanding multiplication is crucial for grasping algebraic concepts. It forms the basis for solving equations, simplifying expressions, and working with variables. The ability to quickly and accurately calculate 6 x 4 contributes to a stronger foundation in algebra and beyond.
-
Geometry and Area Calculation: Multiplication is fundamental in geometry, particularly when calculating area. The area of a rectangle is determined by multiplying its length and width. A rectangle with a length of 6 units and a width of 4 units will have an area of 24 square units, directly reflecting the result of 6 x 4.
-
Real-World Applications: Multiplication is pervasive in our daily lives. From calculating the total cost of multiple items to determining the number of tiles needed for a floor, multiplication simplifies many tasks. For example, if you need six packs of apples, and each pack contains four apples, you'll have a total of 24 apples. Understanding 6 x 4 allows for quick and accurate calculations in such scenarios.
-
Ratio and Proportion: Multiplication is essential when working with ratios and proportions. If the ratio of boys to girls in a class is 6:4, understanding the multiplication involved allows for scaling the ratio to larger or smaller class sizes while maintaining the same proportion.
-
Advanced Mathematical Concepts: The understanding of multiplication lays a solid foundation for more advanced concepts such as exponents, logarithms, and calculus. These concepts, while significantly more complex, all rely on a thorough understanding of fundamental arithmetic operations, including multiplication.
Expanding the Concept: Exploring Factors and Multiples
Understanding 6 x 4 also allows us to explore related mathematical concepts:
-
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. In the equation 6 x 4 = 24, both 6 and 4 are factors of 24. Other factors of 24 include 1, 2, 3, 8, 12, and 24.
-
Multiples: Multiples are numbers obtained by multiplying a specific number by integers. 24 is a multiple of 6 and a multiple of 4. Other multiples of 6 include 6, 12, 18, 24, 30, and so on. Similarly, multiples of 4 are 4, 8, 12, 16, 20, 24, and so on.
Exploring factors and multiples enhances a deeper understanding of numerical relationships and provides valuable insights into number theory.
Frequently Asked Questions (FAQ)
Q: What is the inverse operation of multiplication?
A: The inverse operation of multiplication is division. Just as 6 x 4 = 24, 24 ÷ 4 = 6 and 24 ÷ 6 = 4.
Q: How can I improve my multiplication skills?
A: Consistent practice is key. Use flashcards, practice worksheets, online games, and real-world applications to reinforce your understanding. Focus on memorizing multiplication tables and understanding the different methods for solving multiplication problems.
Q: Why is multiplication important?
A: Multiplication is a fundamental building block in mathematics and is used extensively in everyday life. It allows us to efficiently solve problems involving repeated addition, calculate areas, understand ratios and proportions, and build a strong foundation for more advanced mathematical concepts.
Q: Are there different ways to write 6 x 4?
A: Yes, there are several ways to represent multiplication:
- 6 x 4
- 6 * 4
- 6(4)
- (6)(4)
Conclusion: Mastering the Fundamentals
The seemingly simple question "What is 6 times 4?" leads us down a path of exploring fundamental mathematical principles, practical applications, and the foundational role of multiplication in building a strong mathematical understanding. By understanding the different methods for solving this seemingly basic equation, we gain a deeper appreciation for the power and versatility of multiplication. Mastering this fundamental concept is crucial for success in mathematics and various aspects of everyday life, opening doors to more advanced mathematical exploration and real-world problem-solving. Remember, the journey of understanding mathematics begins with mastering the basics – and 6 times 4 is a perfect place to start.
Latest Posts
Latest Posts
-
Example Of A Compressional Wave
Sep 22, 2025
-
Relationship Between Energy And Wavelength
Sep 22, 2025
-
Is 5 6 A Natural Number
Sep 22, 2025
-
Indian States And State Animals
Sep 22, 2025
-
Flowers Blowing In The Wind
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Times 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.