Is -5/6 A Natural Number
seoindie
Sep 22, 2025 · 6 min read
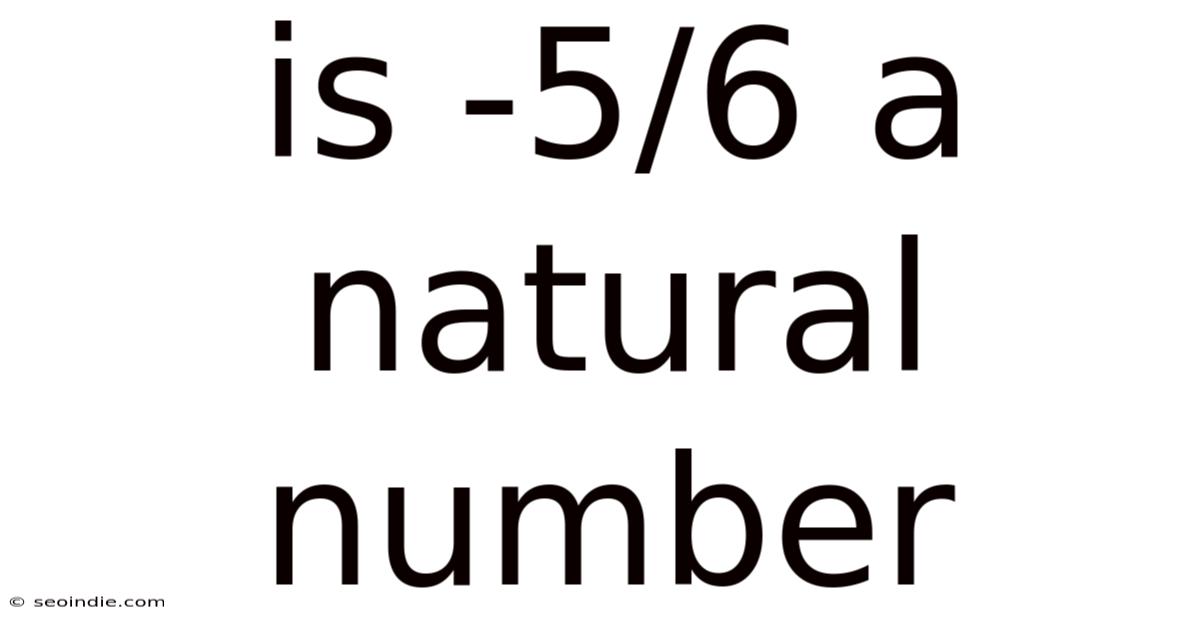
Table of Contents
Is -5/6 a Natural Number? A Deep Dive into Number Systems
Is -5/6 a natural number? The simple answer is no. Understanding why requires a journey into the fascinating world of number systems. This article will explore the different sets of numbers, define natural numbers, and explain why fractions and negative numbers are excluded from this fundamental set. We'll also delve into the properties that distinguish natural numbers and explore related mathematical concepts. By the end, you'll not only know the answer to the initial question but also have a firm grasp of the foundational building blocks of mathematics.
Introduction to Number Systems
Mathematics is built upon a hierarchy of number systems, each extending and refining the previous one. Understanding these systems is crucial for grasping the meaning and properties of various numbers. Let's briefly explore some key sets:
-
Natural Numbers (ℕ): These are the counting numbers, starting from 1 and extending infinitely: {1, 2, 3, 4, 5,...}. They are the foundation upon which other number systems are built. They are used to count discrete objects.
-
Whole Numbers (ℤ₀): This set includes all natural numbers and zero: {0, 1, 2, 3, 4, 5,...}. The addition of zero allows for the representation of the absence of quantity.
-
Integers (ℤ): This set encompasses all whole numbers and their negative counterparts: {..., -3, -2, -1, 0, 1, 2, 3,...}. Integers allow us to represent quantities in opposite directions or debt/credit scenarios.
-
Rational Numbers (ℚ): This set includes all numbers that can be expressed as a fraction p/q, where p and q are integers and q ≠ 0. Rational numbers include integers, fractions, and terminating or repeating decimals. Examples include 1/2, -3/4, 0.75, and 2. Note that integers can be expressed as rational numbers (e.g., 2 can be expressed as 2/1).
-
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Examples include π (pi) and √2.
-
Real Numbers (ℝ): This set encompasses all rational and irrational numbers. It represents all numbers on the number line.
-
Complex Numbers (ℂ): This set includes real numbers and imaginary numbers (numbers involving the imaginary unit i, where i² = -1).
Defining Natural Numbers
Natural numbers, often denoted by ℕ, are the most basic set of numbers. They are the numbers we use for counting discrete objects. The defining characteristics of natural numbers are:
-
Positive: Natural numbers are always positive. They do not include zero or negative values.
-
Integers: Natural numbers are always whole numbers; they do not include fractions or decimals.
-
Discrete: Natural numbers represent distinct, separate units. You can't have 2.5 apples as a natural number; you either have 2 or 3.
-
Ordered: Natural numbers are arranged in a specific order, starting from 1 and increasing infinitely.
-
Counting: Their primary function is to count.
Why -5/6 is Not a Natural Number
Given the definition of natural numbers, it's clear why -5/6 is not a member of this set:
-
Negative Value: -5/6 is a negative number. Natural numbers are exclusively positive.
-
Fractional Value: -5/6 is a fraction, representing a part of a whole. Natural numbers are whole numbers.
Therefore, -5/6 belongs to the set of rational numbers (ℚ) because it can be expressed as a fraction of two integers (-5 and 6), but it does not belong to the set of natural numbers (ℕ).
Further Exploration of Number System Properties
Let's delve deeper into the properties that distinguish natural numbers from other number sets:
-
Closure under Addition: The sum of any two natural numbers is always another natural number. For example, 2 + 3 = 5. This is not true for all number sets. For example, subtracting a larger natural number from a smaller one results in a negative integer.
-
Closure under Multiplication: The product of any two natural numbers is always another natural number. For example, 2 x 3 = 6.
-
Commutative Property: The order of addition or multiplication does not affect the result. For example, 2 + 3 = 3 + 2 and 2 x 3 = 3 x 2.
-
Associative Property: The grouping of numbers in addition or multiplication does not affect the result. For example, (2 + 3) + 4 = 2 + (3 + 4) and (2 x 3) x 4 = 2 x (3 x 4).
-
Distributive Property: Multiplication distributes over addition. For example, 2 x (3 + 4) = (2 x 3) + (2 x 4).
These properties are fundamental to arithmetic operations within the natural number system. However, not all these properties hold true for other number sets.
Illustrative Examples
Let's examine more examples to solidify our understanding:
-
Is 0 a natural number? No, 0 is a whole number but not a natural number.
-
Is 1 a natural number? Yes, 1 is the smallest natural number.
-
Is 3.14 a natural number? No, 3.14 is a rational number (it can be expressed as a fraction) but not a whole number.
-
Is -10 a natural number? No, -10 is an integer but not a natural number.
-
Is √9 a natural number? Yes, because √9 = 3, which is a natural number.
-
Is 1/3 a natural number? No, 1/3 is a rational number but not a whole number.
Frequently Asked Questions (FAQ)
Q: What is the significance of natural numbers in mathematics?
A: Natural numbers are the foundation of arithmetic. They are the first numbers we learn to count with and form the basis for more complex number systems and mathematical concepts.
Q: Are all whole numbers natural numbers?
A: No, all natural numbers are whole numbers, but not all whole numbers are natural numbers (0 is a whole number but not a natural number).
Q: Are natural numbers finite or infinite?
A: Natural numbers are infinite; they extend without end.
Q: What is the difference between rational and irrational numbers?
A: Rational numbers can be expressed as a fraction of two integers, while irrational numbers cannot.
Q: Can negative numbers be used for counting?
A: While not directly used for counting objects in the traditional sense, negative numbers are essential in representing concepts like debt, temperature below zero, or positions on a number line relative to a reference point.
Conclusion
To reiterate, -5/6 is definitively not a natural number. Natural numbers are exclusively positive integers used for counting. -5/6, being both negative and fractional, belongs to the broader set of rational numbers. Understanding the distinctions between different number systems is fundamental to a solid grasp of mathematical principles. This comprehensive exploration should solidify your understanding not only of why -5/6 is not a natural number but also of the fundamental building blocks of the mathematical world. The careful examination of properties and illustrative examples reinforces the concept and allows for a deeper appreciation of the hierarchy and characteristics of the various number systems.
Latest Posts
Latest Posts
-
Metric Units Of Volume Chart
Sep 22, 2025
-
Particle Size Of A Suspension
Sep 22, 2025
-
Perimeter And Area Formula Sheet
Sep 22, 2025
-
Example Of A Lipid Polymer
Sep 22, 2025
-
Group 7a On Periodic Table
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is -5/6 A Natural Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.