Lcm Of 8 And 30
seoindie
Sep 13, 2025 · 5 min read
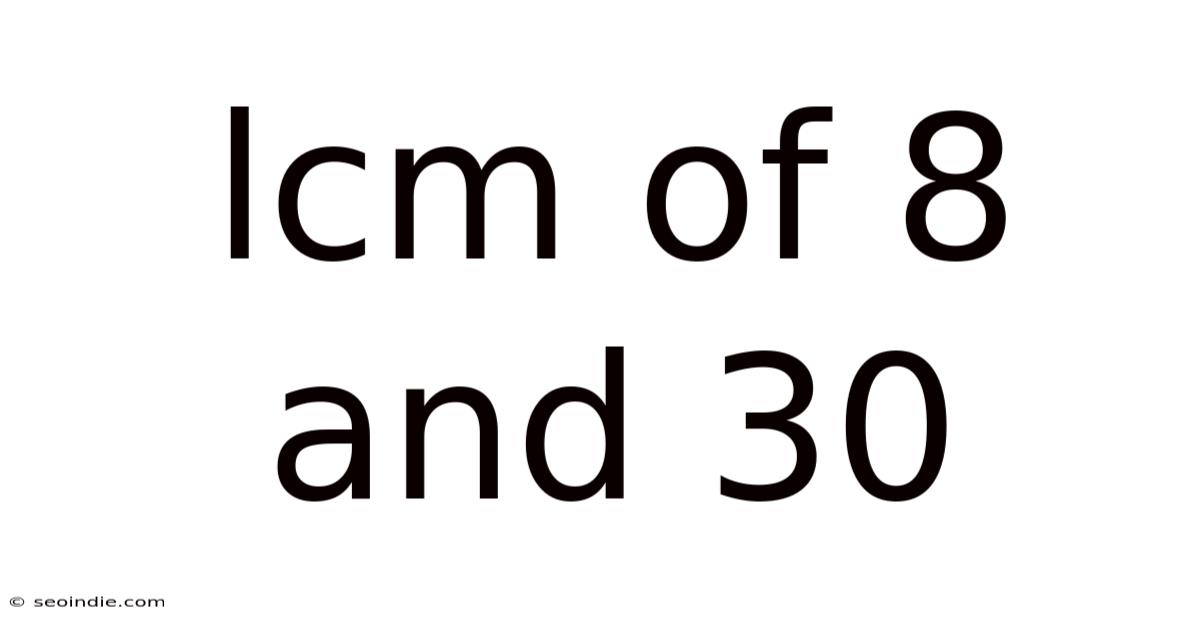
Table of Contents
Finding the LCM of 8 and 30: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for solving various problems involving fractions, ratios, and cyclical events. This article will comprehensively explore how to calculate the LCM of 8 and 30, explaining different methods and delving into the underlying mathematical principles. We'll also look at the practical applications of LCM and address frequently asked questions. Understanding LCMs is essential for students and anyone working with numbers regularly. Let's dive in!
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8 and 30, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so forth. The least common multiple, therefore, is 6.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple that appears in both lists.
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 60, 72, 80, 96, 120...
Multiples of 30: 30, 60, 90, 120, 150...
By comparing the two lists, we can see that the smallest number that appears in both lists is 120. Therefore, the LCM of 8 and 30 is 120.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
- Prime Factorization of 8: 2 x 2 x 2 = 2³
- Prime Factorization of 30: 2 x 3 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either factorization.
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2³ = 8.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Now, we multiply these highest powers together: 2³ x 3 x 5 = 8 x 3 x 5 = 120. Therefore, the LCM of 8 and 30 is 120. This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, we need to find the GCD of 8 and 30. We can use the Euclidean algorithm for this:
- Divide the larger number (30) by the smaller number (8): 30 ÷ 8 = 3 with a remainder of 6.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (6): 8 ÷ 6 = 1 with a remainder of 2.
- Repeat: 6 ÷ 2 = 3 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Now, we can use the formula:
LCM(8, 30) x GCD(8, 30) = 8 x 30 LCM(8, 30) x 2 = 240 LCM(8, 30) = 240 ÷ 2 = 120
Practical Applications of LCM
The concept of LCM has several practical applications across various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 8 minutes, and the other arrives every 30 minutes. Finding the LCM (120 minutes) tells us when both buses will arrive at the stop simultaneously again.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps determine the least common denominator (LCD), simplifying the calculation.
-
Cyclical Events: In scenarios involving repeating cycles, such as planetary orbits or machine cycles, the LCM helps determine when these cycles will align or repeat simultaneously.
-
Project Management: If different tasks in a project have varying completion times, LCM can help determine the shortest time it takes for all tasks to complete a full cycle.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers?
A1: The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all prime factors from all numbers and take the highest power of each. For the listing method, it becomes more cumbersome but still possible.
Q2: Is there a formula for LCM that doesn't involve GCD?
A2: While the GCD method provides an elegant solution, the prime factorization method directly calculates the LCM without explicitly finding the GCD.
Q3: Can the LCM of two numbers be smaller than either of the numbers?
A3: No. The LCM will always be greater than or equal to the largest of the two numbers.
Q4: What if one of the numbers is zero?
A4: The LCM of any number and zero is undefined.
Q5: How can I check my answer?
A5: Once you've calculated the LCM, verify that it is divisible by both original numbers without any remainder.
Conclusion
Finding the LCM of 8 and 30, whether through listing multiples, prime factorization, or using the GCD, consistently yields the result of 120. Understanding the different methods provides flexibility in tackling various problems involving LCMs. The concept is crucial not just for solving mathematical problems but also for addressing real-world scenarios involving cycles, scheduling, and fraction operations. Mastering LCM calculations is a valuable skill for students and anyone dealing with numerical computations. Remember to choose the method most suitable to the situation and always double-check your answer to ensure accuracy. The key is to understand the underlying principles and apply the most efficient method for the task at hand. This knowledge equips you to tackle more complex mathematical problems with confidence.
Latest Posts
Latest Posts
-
What Has Four Letters Riddle
Sep 13, 2025
-
Lcm Of 16 And 28
Sep 13, 2025
-
What Is A Kinetic Friction
Sep 13, 2025
-
List Of Factors Of 48
Sep 13, 2025
-
Lcm Of 35 And 28
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.