Lcm Of 16 And 28
seoindie
Sep 13, 2025 · 6 min read
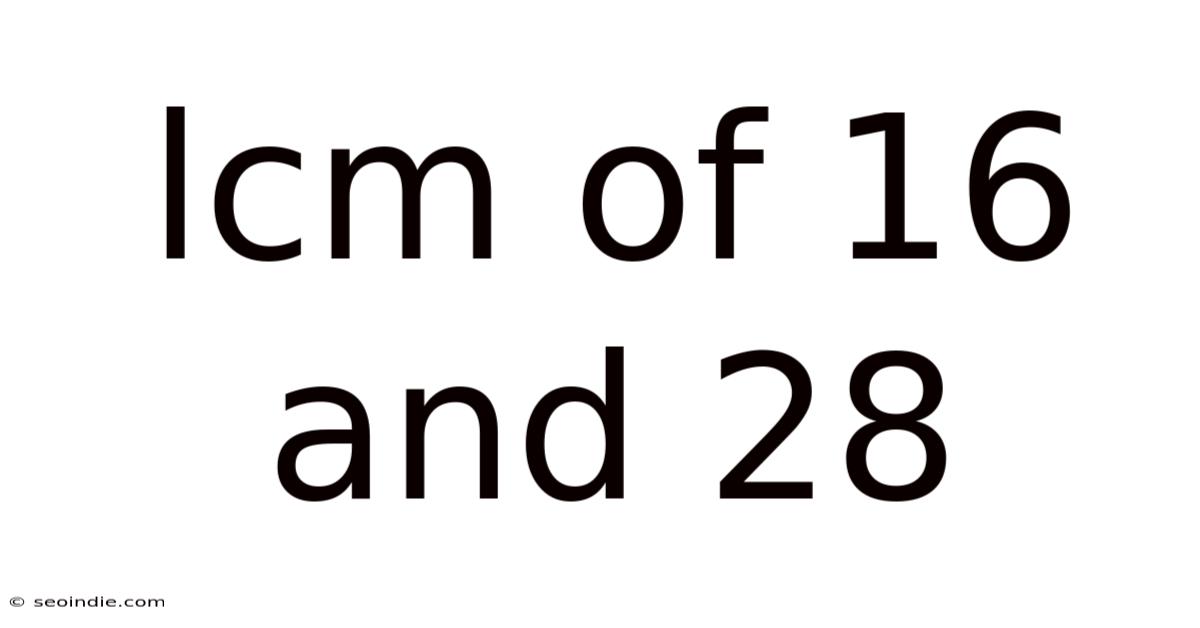
Table of Contents
Finding the Least Common Multiple (LCM) of 16 and 28: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods to calculate it can significantly improve your mathematical skills. This comprehensive guide will explore various approaches to determine the LCM of 16 and 28, delve into the theoretical foundations, and equip you with the knowledge to tackle similar problems with confidence. We'll also touch upon real-world applications where finding the LCM proves invaluable.
Introduction: What is the LCM?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers in question as factors. Understanding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving cycles (like gears or schedules), and more. This article focuses on finding the LCM of 16 and 28, illustrating multiple methods to solve this and similar problems.
Method 1: Listing Multiples
This is the most straightforward approach, especially for smaller numbers. We simply list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224...
- Multiples of 28: 28, 56, 84, 112, 140, 168, 196, 224, 252...
Notice that the smallest multiple present in both lists is 112. Therefore, the LCM of 16 and 28 is 112.
This method is efficient for smaller numbers but becomes increasingly cumbersome as the numbers grow larger. Let's explore more efficient methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique that breaks down a number into its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers.
-
Prime Factorization of 16: 16 = 2 x 2 x 2 x 2 = 2⁴
-
Prime Factorization of 28: 28 = 2 x 2 x 7 = 2² x 7
-
Finding the LCM: To find the LCM using prime factorization, we identify the highest power of each prime factor present in either factorization. In this case, we have:
- The highest power of 2 is 2⁴ = 16
- The highest power of 7 is 7¹ = 7
-
Calculate the LCM: Multiply the highest powers of all prime factors together: LCM(16, 28) = 2⁴ x 7 = 16 x 7 = 112
This method is more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic approach and a deeper understanding of the underlying number theory.
Method 3: Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) is the largest positive integer that divides both numbers without leaving a remainder. There's a convenient relationship between the LCM and GCD of two numbers:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Finding the GCD of 16 and 28: We can use the Euclidean algorithm to find the GCD efficiently.
- 28 = 1 x 16 + 12
- 16 = 1 x 12 + 4
- 12 = 3 x 4 + 0
The last non-zero remainder is 4, so the GCD(16, 28) = 4.
-
Calculating the LCM: Now, we apply the formula:
LCM(16, 28) = (16 x 28) / 4 = 448 / 4 = 112
This method showcases the elegant connection between the LCM and GCD, offering an alternative approach for calculating the LCM.
Method 4: Ladder Method (or Staircase Method)
This visual method is helpful for understanding the process. We write the numbers side-by-side and repeatedly divide them by their common factors until we're left with only 1s. The LCM is the product of all the divisors and the remaining numbers.
2 | 16 28
2 | 8 14
2 | 4 7
| 2 7
| 1 7
| 1 1
LCM = 2 x 2 x 2 x 7 = 112
Explanation of the Methods and Their Efficiency
Each method offers a unique perspective on finding the LCM. The listing multiples method is intuitive but impractical for larger numbers. Prime factorization provides a structured approach, particularly efficient for larger numbers with many factors. The GCD method elegantly utilizes the relationship between LCM and GCD, offering an efficient alternative. The ladder method provides a visual representation of the process. The choice of method depends on the context and the size of the numbers involved. For smaller numbers, listing multiples or the ladder method might suffice. For larger numbers, prime factorization or the GCD method are more efficient and less prone to errors.
Real-World Applications of LCM
The concept of LCM isn't confined to theoretical mathematics; it has practical applications in various fields:
-
Scheduling: Imagine two buses arriving at a station, one every 16 minutes and the other every 28 minutes. The LCM (112 minutes) tells us when both buses will arrive at the station simultaneously.
-
Gear Ratios: In mechanics, gear ratios often involve LCM calculations to determine the optimal gear combinations for smooth operation.
-
Project Management: Tasks that repeat with different cycles can be synchronized using LCM to plan optimal schedules.
-
Music: The LCM is used to find the least common denominator for musical notes, ensuring harmonious melodies.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two numbers? A: The same methods can be extended to more than two numbers. For prime factorization, you'd consider all prime factors and their highest powers. For the GCD method, you'd need to find the GCD of all numbers iteratively.
-
Q: What if the numbers are negative? A: The LCM is always positive. You should find the LCM of the absolute values of the numbers.
-
Q: Is there a formula for finding the LCM of three or more numbers? A: There isn't a single compact formula like the one for two numbers, but the prime factorization method generalizes easily. You find the prime factorization of each number and take the highest power of each prime factor present across all numbers.
Conclusion
Finding the LCM of 16 and 28, as we've demonstrated, can be approached using several methods. The most suitable method depends on the complexity of the problem and your preference. Understanding the underlying principles of prime factorization and the relationship between LCM and GCD significantly enhances your ability to solve these problems efficiently. Mastering these concepts empowers you to tackle more complex mathematical challenges and apply them to various real-world scenarios. Remember to practice and explore different methods to develop your mathematical intuition and strengthen your problem-solving skills. The LCM, seemingly a simple concept, unveils deeper connections within number theory and provides practical solutions across various disciplines.
Latest Posts
Latest Posts
-
Isothermal Process And Adiabatic Process
Sep 13, 2025
-
Is 30 An Even Number
Sep 13, 2025
-
Multiplication Of Fractions Problem Solving
Sep 13, 2025
-
Items That Start With D
Sep 13, 2025
-
Potassium Hydroxide Weak Or Strong
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 16 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.