Lcm Of 60 And 45
seoindie
Sep 16, 2025 · 6 min read
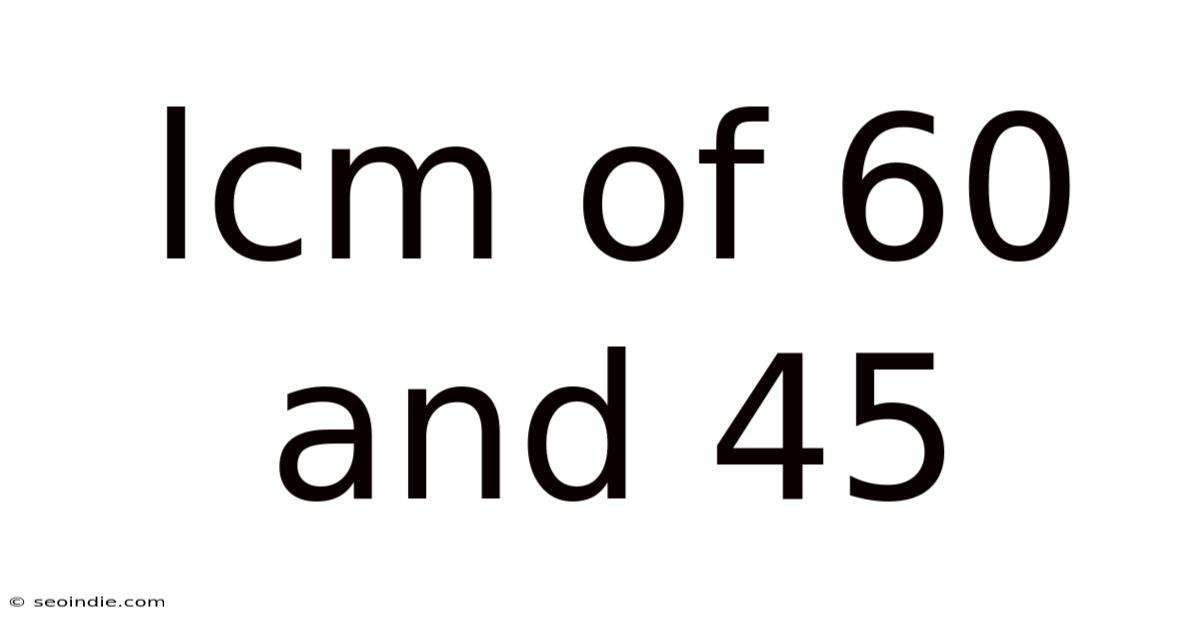
Table of Contents
Finding the Least Common Multiple (LCM) of 60 and 45: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving real-world problems involving cycles and repetitions. This article provides a thorough exploration of how to calculate the LCM of 60 and 45, employing multiple methods to solidify understanding. We'll delve into the underlying principles, demonstrate different approaches, and address frequently asked questions. Understanding LCMs is key to mastering more advanced mathematical concepts.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number that is divisible by both 2 and 3. This concept is widely used in various mathematical operations and real-world scenarios involving cyclical events or shared factors. This article will focus on finding the LCM of 60 and 45, illustrating different methods suitable for diverse mathematical backgrounds.
Method 1: Listing Multiples
This method is straightforward and easy to visualize, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 60: 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, ...
Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360, 405, 450, ...
By comparing the lists, we observe that the smallest multiple common to both 60 and 45 is 180. Therefore, the LCM(60, 45) = 180. This method is effective for smaller numbers, but it becomes less efficient as the numbers grow larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Prime Factorization of 60:
60 = 2 x 30 = 2 x 2 x 15 = 2 x 2 x 3 x 5 = 2² x 3 x 5
Prime Factorization of 45:
45 = 5 x 9 = 5 x 3 x 3 = 3² x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Now, we multiply these highest powers together:
LCM(60, 45) = 2² x 3² x 5 = 4 x 9 x 5 = 180
This method is more systematic and works effectively for larger numbers where listing multiples would be impractical.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. We can use this relationship to find the LCM if we know the GCD.
First, let's find the GCD of 60 and 45 using the Euclidean algorithm:
60 = 1 x 45 + 15 45 = 3 x 15 + 0
The last non-zero remainder is the GCD, which is 15. Now, we can use the formula:
LCM(60, 45) x GCD(60, 45) = 60 x 45 LCM(60, 45) x 15 = 2700 LCM(60, 45) = 2700 / 15 = 180
Method 4: Using the Formula for LCM with GCD (Alternative Approach)
A slightly different way to utilize the relationship between LCM and GCD is to directly calculate the LCM using the prime factorizations of both numbers and the GCD:
- Find the prime factorization of both numbers: As calculated before: 60 = 2² x 3 x 5 and 45 = 3² x 5
- Find the GCD: The common factors are 3 and 5. The lowest power of the common factors is 3¹ and 5¹. Thus, GCD(60,45) = 3 x 5 = 15
- Apply the formula: LCM(a, b) = (a x b) / GCD(a, b). Substituting the values: LCM(60, 45) = (60 x 45) / 15 = 2700 / 15 = 180
Illustrative Real-World Example
Imagine you have two conveyor belts. One belt moves every 60 seconds, and the other moves every 45 seconds. You want to know when both belts will be at the starting point simultaneously again. This is where the LCM comes in. The LCM(60, 45) = 180 seconds. Both belts will return to their starting point at the same time after 180 seconds (or 3 minutes).
Explanation of the Mathematical Principles Involved
The methods presented rely on fundamental number theory concepts:
- Prime Factorization: Every integer greater than 1 can be uniquely expressed as a product of prime numbers. This unique factorization is the cornerstone of many number theory concepts.
- Greatest Common Divisor (GCD): The GCD of two or more integers is the largest integer that divides all of them without leaving a remainder. The Euclidean algorithm is an efficient method for finding the GCD.
- Relationship between LCM and GCD: The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This fundamental relationship allows for efficient calculation of the LCM when the GCD is known.
Frequently Asked Questions (FAQ)
-
Q: Is there only one LCM for two numbers? A: Yes, there is only one least common multiple for any given pair of numbers.
-
Q: What if one of the numbers is zero? A: The LCM of any number and zero is undefined.
-
Q: Can I use a calculator to find the LCM? A: Many scientific and graphing calculators have built-in functions to compute the LCM of two or more numbers.
-
Q: What if I have more than two numbers? A: The methods described can be extended to find the LCM of more than two numbers. For prime factorization, you'd consider all prime factors and their highest powers. For the GCD-based method, you'd need to iteratively compute the LCM of pairs of numbers.
Conclusion
Finding the least common multiple is a versatile skill applicable in various mathematical contexts and real-world problems. This article has presented multiple methods—listing multiples, prime factorization, and using the GCD—for calculating the LCM, demonstrating their efficiency and application. Understanding these methods equips you with a deeper comprehension of fundamental number theory and its practical implications. Mastering the calculation of LCMs is essential for further exploration of more complex mathematical concepts and their applications in various fields. Remember to choose the method best suited to the given numbers and your comfort level with mathematical concepts. The consistent application of these methods will build a strong foundation in number theory.
Latest Posts
Latest Posts
-
Metallic Minerals And Nonmetallic Minerals
Sep 16, 2025
-
Hardest Tissue Of The Body
Sep 16, 2025
-
3 Meters How Many Inches
Sep 16, 2025
-
What Are Measures Of Dispersion
Sep 16, 2025
-
Is 3 0 A Whole Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 60 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.