Lcm Of 6 12 15
seoindie
Sep 22, 2025 · 6 min read
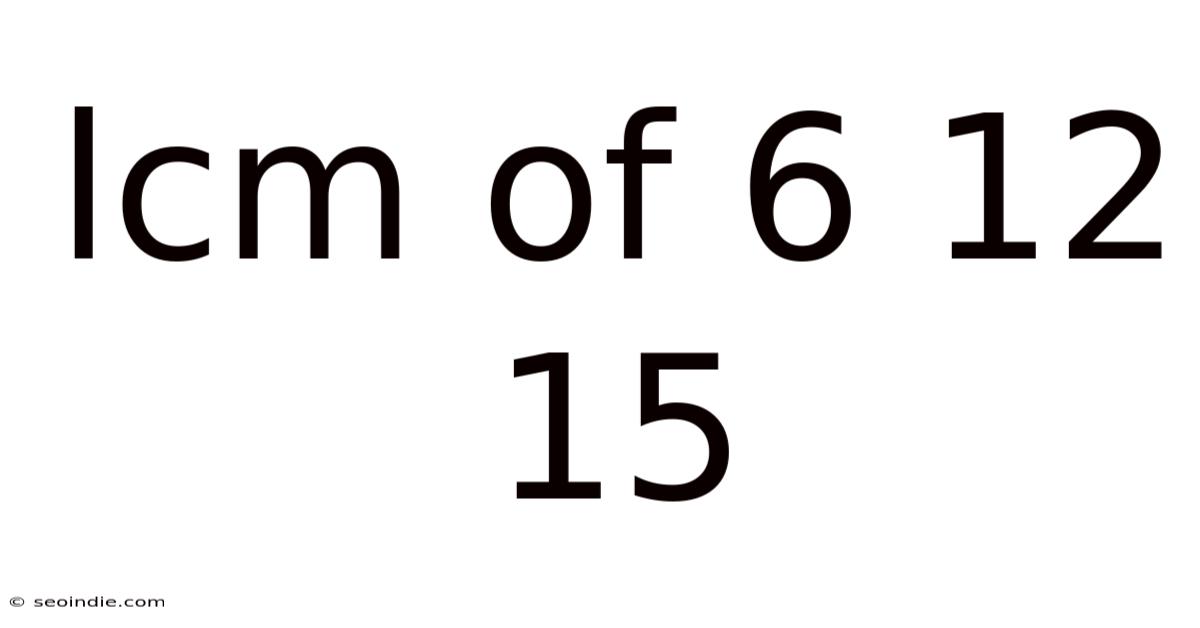
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 12, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can significantly enhance your mathematical skills and problem-solving abilities. This article provides a thorough explanation of how to find the LCM of 6, 12, and 15, exploring various techniques and delving into the theoretical foundations. We'll move beyond simply finding the answer and explore the 'why' behind the calculations, making this a valuable resource for students and anyone wanting to strengthen their understanding of LCM.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 6, 12, and 15, let's define what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. This concept is fundamental in various areas of mathematics, including fractions, simplifying expressions, and solving problems involving ratios and proportions.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 60, ...
- Multiples of 12: 12, 24, 36, 48, 60, ...
- Multiples of 15: 15, 30, 45, 60, ...
By comparing these lists, we can see that the smallest number that appears in all three lists is 60. Therefore, the LCM of 6, 12, and 15 is 60.
This method is simple to understand but can become cumbersome and time-consuming when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – the smallest prime numbers that multiply together to give the original number.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime Factorization of 15: 3 x 5
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 4 x 3 x 5 = 60. Therefore, the LCM of 6, 12, and 15 is 60.
This method is more efficient than listing multiples, particularly when dealing with larger numbers. It provides a systematic approach that avoids the potential for overlooking common multiples.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
This formula works only if you have the GCD of all the numbers. Let's apply this to our example:
-
Find the GCD of 6, 12, and 15: The GCD of 6, 12, and 15 is 3 (the largest number that divides all three).
-
Apply the formula: LCM(6, 12, 15) = (6 x 12 x 15) / 3 = 1080 / 3 = 360.
Wait a minute! This gives us 360, not 60, which we found using the previous methods. This is because the formula provided is incorrect if more than two numbers are involved. The formula LCM(a,b) = (a*b)/GCD(a,b) is only valid for two numbers. For more than two numbers, the method using prime factorization is the most reliable.
Method 4: Ladder Method (or Staircase Method)
This method is a visual approach, particularly helpful for visualizing the process. It's essentially a systematic way of finding the prime factors.
2 | 6 12 15
2 | 3 6 15
3 | 3 3 15
5 | 1 1 5
| 1 1 1
We repeatedly divide the numbers by the smallest prime number that divides at least one of them. We continue until we reach all 1s. The LCM is the product of all the divisors on the left side: 2 x 2 x 3 x 5 = 60.
Why is understanding LCM important?
Understanding LCM is crucial for several mathematical concepts and real-world applications:
-
Fraction Operations: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. This allows you to find a common denominator and perform the operation correctly.
-
Solving Ratio and Proportion Problems: LCM helps in determining equivalent ratios and solving problems involving proportional relationships.
-
Scheduling and Time Management: LCM is used to determine when events with different repeating cycles will occur simultaneously. For example, if two machines operate on cycles of 6 and 12 hours, their LCM will tell you when they will both be at their starting point simultaneously.
-
Modular Arithmetic: LCM is fundamental in modular arithmetic, which is used in cryptography and computer science.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have no common factors?
If the numbers are relatively prime (meaning their GCD is 1), their LCM is simply the product of the numbers. For example, the LCM of 7 and 15 (which have a GCD of 1) is 7 x 15 = 105.
Q2: Can I use a calculator to find the LCM?
Many scientific calculators have a built-in function to calculate the LCM of multiple numbers. However, understanding the methods outlined above is crucial for comprehending the underlying mathematical principles.
Q3: Are there other methods for finding the LCM?
While the methods explained above are the most common and effective, other algorithms exist, particularly for computational purposes with very large numbers. These often involve sophisticated number theory concepts.
Q4: What happens if one of the numbers is zero?
The LCM of any set of numbers that includes zero is undefined because zero is divisible by any number.
Conclusion
Finding the least common multiple (LCM) of 6, 12, and 15, as demonstrated, yields a result of 60. We explored several methods – listing multiples, prime factorization, and the ladder method – each offering a different approach to solving this type of problem. Understanding these methods provides a strong foundation for tackling more complex LCM problems and reinforces your understanding of fundamental number theory concepts. Remember, the prime factorization method is the most robust and efficient approach, especially when dealing with larger numbers or a greater number of integers. The ability to calculate LCM is a valuable skill that extends beyond the classroom, finding application in diverse fields and problem-solving scenarios.
Latest Posts
Latest Posts
-
Is 361 A Perfect Square
Sep 22, 2025
-
All The Factors Of 85
Sep 22, 2025
-
5 Square Root Of 2
Sep 22, 2025
-
Words That Start With Tac
Sep 22, 2025
-
Words That Start With On
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.