Lcm Of 56 And 84
seoindie
Sep 25, 2025 · 5 min read
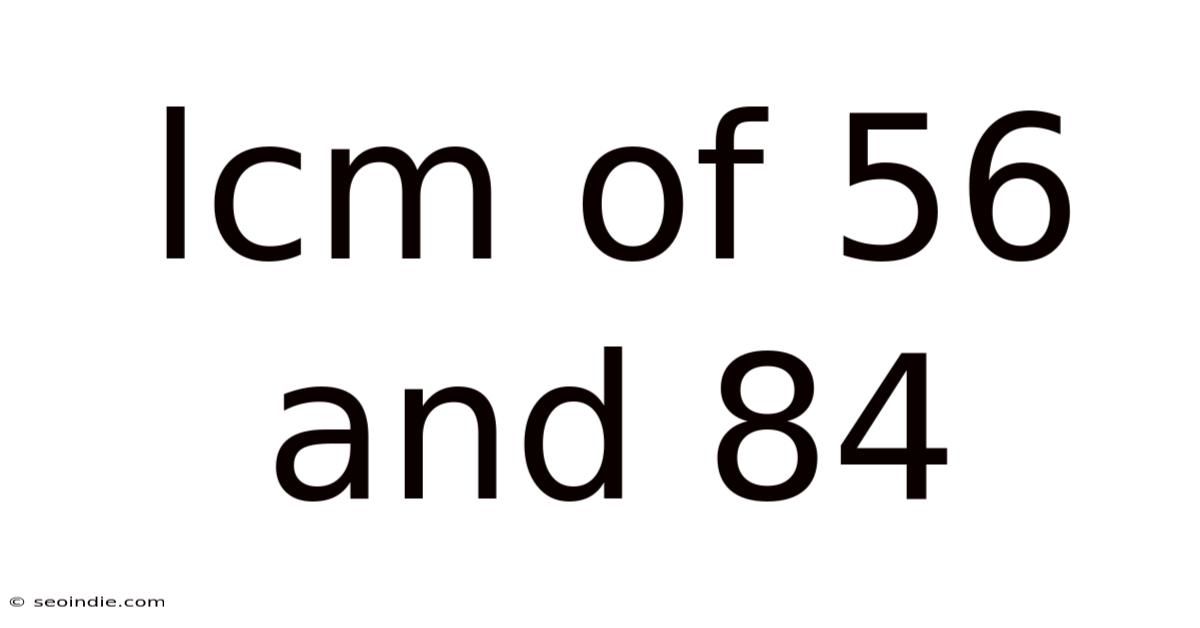
Table of Contents
Finding the LCM of 56 and 84: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving real-world problems involving cycles or timing. This comprehensive guide will walk you through different methods to calculate the LCM of 56 and 84, explaining the underlying principles and providing a deeper understanding of the concept itself. Understanding LCM goes beyond simply finding the answer; it's about grasping the mathematical relationships between numbers. This article will equip you with the knowledge to confidently tackle LCM problems of any complexity.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify the definition of LCM. The least common multiple of two or more numbers is the smallest positive integer that is divisible by all the numbers. In simpler terms, it's the smallest number that is a multiple of both numbers. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number that is divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 56 and 84, involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 56: 56, 112, 168, 224, 280, 336, 392, 448, 504, 560...
- Multiples of 84: 84, 168, 252, 336, 420, 504, 588, 672, 756, 840...
By comparing the lists, we can see that the smallest number appearing in both lists is 168. Therefore, the LCM of 56 and 84 is 168.
This method is simple and intuitive but can become cumbersome for larger numbers. It's best suited for smaller numbers where the lists remain manageable.
Method 2: Prime Factorization
This method offers a more efficient approach, especially for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 56
56 can be factored as follows:
56 = 2 x 28 = 2 x 2 x 14 = 2 x 2 x 2 x 7 = 2³ x 7¹
Step 2: Prime Factorization of 84
84 can be factored as follows:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3¹ x 7¹
Step 3: Identifying Common and Unique Prime Factors
Now, let's identify the prime factors present in both numbers and note the highest power of each:
- 2: The highest power is 2³ (from 56)
- 3: The highest power is 3¹ (from 84)
- 7: The highest power is 7¹ (from both 56 and 84)
Step 4: Calculating the LCM
The LCM is calculated by multiplying the highest powers of all the unique prime factors:
LCM(56, 84) = 2³ x 3¹ x 7¹ = 8 x 3 x 7 = 168
Therefore, the LCM of 56 and 84 using prime factorization is 168. This method is more efficient and less prone to error than listing multiples, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are intimately related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This provides an alternative method for calculating the LCM.
Step 1: Finding the GCD of 56 and 84
We can use the Euclidean algorithm to find the GCD.
- Divide 84 by 56: 84 = 56 x 1 + 28
- Divide 56 by 28: 56 = 28 x 2 + 0
The last non-zero remainder is 28, so the GCD(56, 84) = 28.
Step 2: Calculating the LCM using the GCD
The formula relating LCM and GCD is:
LCM(a, b) = (a x b) / GCD(a, b)
Substituting the values:
LCM(56, 84) = (56 x 84) / 28 = 4704 / 28 = 168
Therefore, using the GCD method, the LCM of 56 and 84 is 168. This method is particularly useful when the GCD is easily determined.
Real-World Applications of LCM
Understanding LCM is not just an abstract mathematical exercise; it has practical applications in various fields:
- Scheduling: Imagine two buses depart from the same station at different intervals. Finding the LCM of their departure intervals will tell you when they will depart together again.
- Fraction Simplification: When adding or subtracting fractions, finding the LCM of the denominators is essential to find a common denominator.
- Cyclic Processes: In physics and engineering, many processes are cyclical. The LCM helps determine when cycles will coincide or overlap.
- Project Management: In project management, LCM can be used to synchronize tasks with different completion cycles.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both given numbers. The GCD (Greatest Common Divisor) is the largest number that divides both given numbers without leaving a remainder.
Q: Can the LCM of two numbers be smaller than the numbers themselves?
A: No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
Q: Is there a single "best" method for finding the LCM?
A: The best method depends on the numbers involved. For smaller numbers, listing multiples is straightforward. For larger numbers, prime factorization or the GCD method are more efficient.
Q: What if I have more than two numbers?
A: The concept extends to more than two numbers. You can find the LCM of three or more numbers by extending the prime factorization method. Find the prime factorization of each number, then multiply the highest powers of each unique prime factor to find the LCM.
Conclusion
Finding the LCM of 56 and 84, as demonstrated through three different methods, highlights the versatility and importance of this fundamental mathematical concept. Whether you use the listing multiples method, prime factorization, or the GCD approach, understanding the underlying principles ensures you can confidently tackle LCM problems regardless of the numbers' size or complexity. The ability to calculate LCM is a valuable skill with practical implications extending beyond the classroom into various real-world scenarios. Remember that the core concept is about identifying the smallest common multiple—the smallest number divisible by all the given numbers. Mastering this concept opens doors to a deeper appreciation of number theory and its practical applications.
Latest Posts
Latest Posts
-
3 Times What Equals 72
Sep 25, 2025
-
Parallel Vs Antiparallel Beta Sheets
Sep 25, 2025
-
What Does 5cm Look Like
Sep 25, 2025
-
Gene Knockdown Vs Gene Knockout
Sep 25, 2025
-
2 Times What Equals 36
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 56 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.