3 Times What Equals 72
seoindie
Sep 25, 2025 · 5 min read
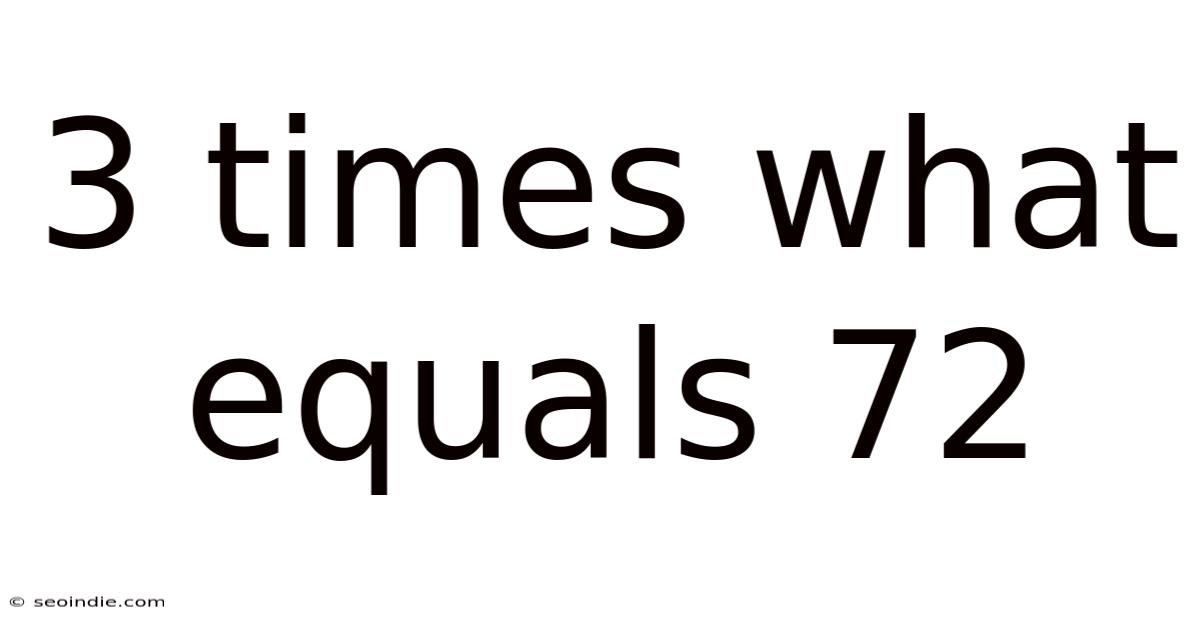
Table of Contents
Decoding 72: Exploring the Multiplicative Pathways to 72
Finding numbers that, when multiplied, equal 72 might seem like a simple arithmetic problem. However, delving into the various factor pairs that yield 72 opens a window into the fascinating world of number theory, revealing patterns, exploring prime factorization, and even touching upon applications in higher-level mathematics. This article will explore the different ways to reach 72 through multiplication, examining the various factor pairs and discussing the underlying mathematical principles. We'll cover everything from basic arithmetic to more advanced concepts, ensuring that this exploration is both insightful and accessible to readers of all mathematical backgrounds.
Understanding Factors and Multiples
Before we dive into the specific factor pairs of 72, let's establish a firm understanding of the fundamental concepts. A factor of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Conversely, a multiple of a number is the result of multiplying that number by any whole number. Multiples of 3 include 3, 6, 9, 12, and so on. In our quest to find the numbers that multiply to 72, we're essentially searching for all the factor pairs of 72.
Finding the Factor Pairs of 72: A Systematic Approach
One way to systematically identify all the factor pairs of 72 is to start with the smallest factor, which is 1. We then ask: "What number multiplied by 1 equals 72?" The answer is 72. This gives us our first factor pair: 1 x 72.
Next, we move to the next smallest factor, 2. "What number multiplied by 2 equals 72?" The answer is 36. This gives us the factor pair: 2 x 36.
We continue this process:
- 3 x 24
- 4 x 18
- 6 x 12
- 8 x 9
Notice that as we progress, the numbers in our factor pairs get closer together. This pattern continues until the factors are mirror images of each other (e.g., 8 x 9 and 9 x 8 are essentially the same factor pair). Once we reach this point, we've identified all the factor pairs. Therefore, the factor pairs of 72 are:
- 1 x 72
- 2 x 36
- 3 x 24
- 4 x 18
- 6 x 12
- 8 x 9
Prime Factorization: The Building Blocks of 72
Prime factorization is a powerful tool in number theory. It involves breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves. This provides a unique representation of the number, much like a DNA fingerprint. Let's find the prime factorization of 72:
We can start by dividing 72 by its smallest prime factor, 2:
72 ÷ 2 = 36
Now, we divide 36 by 2:
36 ÷ 2 = 18
And again:
18 ÷ 2 = 9
Now, we've reached a number that's not divisible by 2 anymore. The next smallest prime number is 3:
9 ÷ 3 = 3
Finally, we have 3, which is a prime number. Therefore, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, or 2³ x 3².
This prime factorization is unique to 72 and can be used to generate all of its factors. Any combination of these prime factors, multiplied together, will result in a factor of 72. This provides a more fundamental understanding of the structure of the number.
Applications and Extensions: Beyond Basic Arithmetic
While finding the factors of 72 might seem like a simple exercise, the underlying concepts have far-reaching applications in various areas of mathematics and beyond:
- Algebra: Understanding factors is crucial for solving algebraic equations, particularly those involving factoring quadratic expressions or simplifying polynomials.
- Geometry: Factors play a role in calculating areas and volumes of shapes. For example, finding the dimensions of a rectangle with an area of 72 square units involves finding factor pairs of 72.
- Combinatorics and Probability: Counting combinations and permutations often involves working with factors and multiples.
- Computer Science: Prime factorization forms the basis of many cryptographic algorithms used to secure online transactions and data.
Frequently Asked Questions (FAQs)
Q: Are there any negative factors of 72?
A: Yes. Since a negative number multiplied by a negative number results in a positive number, we can also consider the negative factor pairs: (-1 x -72), (-2 x -36), (-3 x -24), (-4 x -18), (-6 x -12), and (-8 x -9).
Q: How can I quickly find the factors of a larger number?
A: For larger numbers, using prime factorization can be a more efficient approach. Once you've determined the prime factorization, you can systematically generate all the factors by combining different combinations of the prime factors.
Q: What if I need to find three numbers that multiply to 72?
A: This expands the possibilities significantly! You can start by finding pairs of factors and then see if you can further break down one or both numbers to get a third number. For example, you could take the factor pair 2 x 36 and decompose 36 into 4 x 9, giving you 2 x 4 x 9 = 72. Many combinations are possible.
Q: Is there a formula to find all factors of a number?
A: There isn't a single, straightforward formula to directly list all factors of a number. However, the process of prime factorization and systematically exploring combinations of prime factors provides a reliable method.
Conclusion: The Richness of Number Theory
This exploration of the numbers that multiply to 72 reveals that what initially seems like a simple arithmetic problem actually opens doors to a deeper understanding of number theory and its applications. From the basic concepts of factors and multiples to the more advanced technique of prime factorization, this exercise illustrates the interconnectedness of mathematical ideas and the elegance of their underlying principles. Whether you are a student learning the basics of arithmetic or a more advanced mathematician, exploring the intricacies of number theory can be a rewarding and enriching experience. The journey of understanding how numbers interact and relate to one another is a journey of discovery that extends far beyond the simple question of "3 times what equals 72?"
Latest Posts
Latest Posts
-
3 Times What Equals 72
Sep 25, 2025
-
Parallel Vs Antiparallel Beta Sheets
Sep 25, 2025
-
What Does 5cm Look Like
Sep 25, 2025
-
Gene Knockdown Vs Gene Knockout
Sep 25, 2025
-
2 Times What Equals 36
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.