Lcm Of 5 And 5
seoindie
Sep 20, 2025 · 6 min read
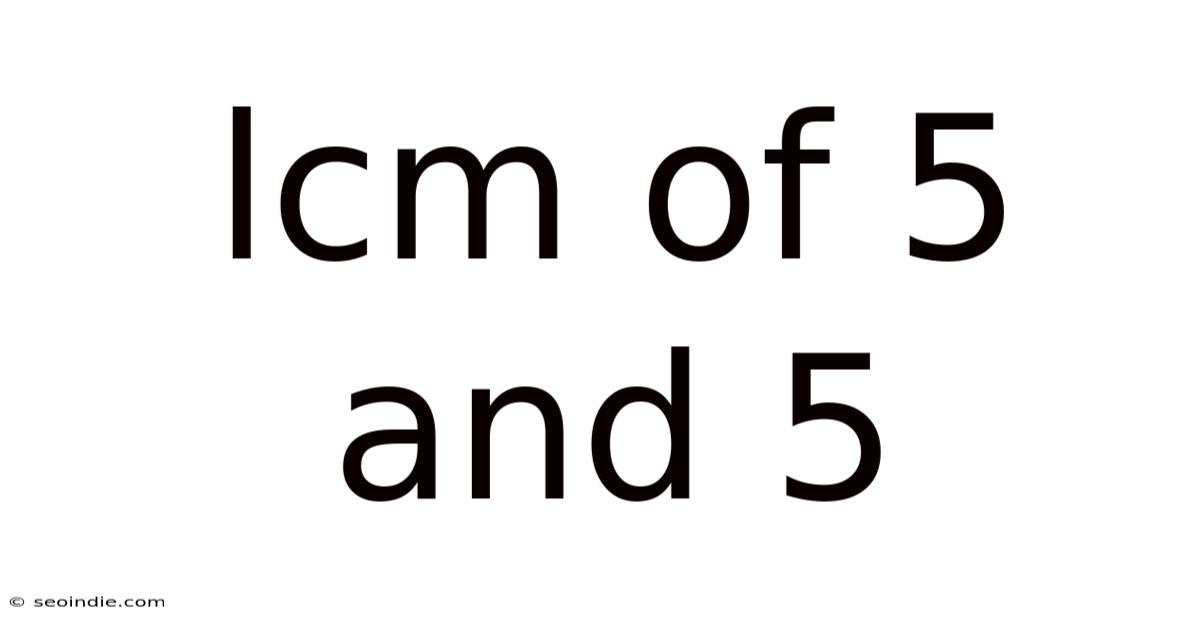
Table of Contents
Finding the Least Common Multiple (LCM) of 5 and 5: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem trivial, especially when dealing with simple numbers like 5 and 5. However, understanding the underlying concepts and exploring different methods to calculate the LCM lays a crucial foundation for more advanced mathematical concepts. This article will delve into the LCM of 5 and 5, explaining various approaches, exploring the theoretical underpinnings, and addressing frequently asked questions. We’ll even expand the discussion to tackle more complex LCM problems, demonstrating the versatility of the methods we explore. This will equip you with a comprehensive understanding of LCM, irrespective of the numbers involved.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. Think of it as finding the smallest common denominator when working with fractions. For instance, if we want to add 1/3 and 1/6, we need to find the LCM of 3 and 6, which is 6. This allows us to rewrite the fractions with a common denominator before adding them.
Calculating the LCM of 5 and 5: The Easiest Case
The LCM of 5 and 5 is exceptionally straightforward. Since both numbers are identical, the LCM is simply 5. There is no smaller positive integer that is divisible by both 5 and 5. This highlights a key property of LCM: the LCM of any number and itself is that number.
Methods for Finding the LCM: Beyond the Obvious
While the LCM of 5 and 5 is immediately apparent, let's explore common methods for calculating the LCM, which are invaluable when dealing with larger or more complex numbers. These methods will be illustrated with examples, building a solid understanding of the process.
1. Listing Multiples Method:
This is a simple, intuitive method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
The smallest common multiple is clearly 5.
2. Prime Factorization Method:
This method is more powerful and efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime Factorization of 5: 5 (5 is a prime number)
- Prime Factorization of 5: 5 (5 is a prime number)
Both numbers have only one prime factor, 5, with a power of 1. Therefore, the LCM is 5¹ = 5.
3. Greatest Common Divisor (GCD) Method:
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both integers without leaving a remainder. The formula linking LCM and GCD is:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 5 and 5. Since both numbers are identical, the GCD is 5. Then, applying the formula:
LCM(5, 5) * GCD(5, 5) = 5 * 5
LCM(5, 5) * 5 = 25
LCM(5, 5) = 25 / 5 = 5
This confirms our previous result.
Expanding the Concept: LCM with Different Numbers
Let's apply the prime factorization method to find the LCM of more complex numbers to solidify our understanding.
Example 1: Finding the LCM of 12 and 18
- Prime factorization of 12: 2² * 3¹
- Prime factorization of 18: 2¹ * 3²
To find the LCM, we take the highest power of each prime factor present: 2² and 3². Therefore, LCM(12, 18) = 2² * 3² = 4 * 9 = 36.
Example 2: Finding the LCM of 24, 36, and 48
- Prime factorization of 24: 2³ * 3¹
- Prime factorization of 36: 2² * 3²
- Prime factorization of 48: 2⁴ * 3¹
The highest powers of the prime factors are 2⁴ and 3². Therefore, LCM(24, 36, 48) = 2⁴ * 3² = 16 * 9 = 144.
The Importance of LCM in Various Applications
Understanding LCM extends far beyond basic arithmetic. It has significant applications in various fields, including:
- Fraction Arithmetic: As mentioned earlier, LCM is crucial for adding and subtracting fractions with different denominators.
- Scheduling Problems: Determining when events will coincide, such as the overlapping of bus schedules or the cyclical repetition of tasks.
- Music Theory: Finding the LCM helps in determining the harmonic intervals between musical notes.
- Engineering and Design: Calculating periodic cycles in machines or systems.
- Computer Science: In algorithms related to synchronization and scheduling processes.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number divisible by both integers, while the GCD (Greatest Common Divisor) is the largest number that divides both integers without leaving a remainder. They are inversely related, as shown in the formula: LCM(a, b) * GCD(a, b) = a * b.
Q: Can the LCM of two numbers be greater than the numbers themselves?
A: Yes, the LCM of two numbers is always greater than or equal to the larger of the two numbers. It will only be equal if the two numbers are the same, as in the case of LCM(5,5)=5. Otherwise, it will be greater.
Q: How do I find the LCM of more than two numbers?
A: The prime factorization method is the most efficient way. Find the prime factorization of each number, then take the highest power of each prime factor present to determine the LCM.
Q: Is there a formula to calculate LCM directly without using prime factorization or GCD?
A: While there isn't a single, universally applicable formula avoiding prime factorization or GCD, iterative methods exist. These methods might involve repeated calculations and are less efficient than the previously discussed methods, especially for larger numbers.
Conclusion: Mastering the LCM
While finding the LCM of 5 and 5 might seem trivial at first glance, delving into the methods and understanding the underlying concepts provides a firm foundation for tackling more complex number theory problems. The prime factorization method offers a powerful and efficient approach for determining the LCM of any set of integers, irrespective of their size. Its applications extend beyond basic arithmetic, playing a crucial role in various mathematical, scientific, and engineering fields. Mastering the concept of LCM is a significant step towards improving your mathematical skills and problem-solving abilities. Remember, the key is to understand the why behind the calculations, not just the how. This deeper understanding will make future mathematical challenges much more manageable.
Latest Posts
Latest Posts
-
Why Voting Is Important Essay
Sep 20, 2025
-
4 Square Root Of 2
Sep 20, 2025
-
Fill In The Missing Numbers
Sep 20, 2025
-
What Is 15 Divisible By
Sep 20, 2025
-
Differentiate Between Heat And Temperature
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.