4/ Square Root Of 2
seoindie
Sep 20, 2025 · 5 min read
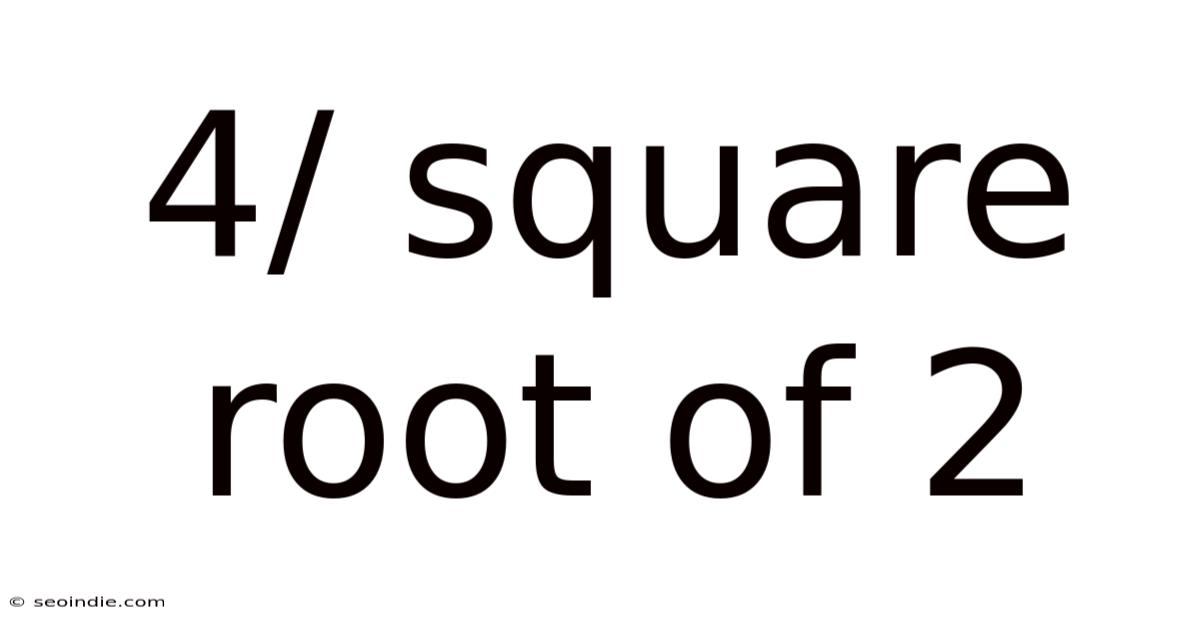
Table of Contents
Decoding 4 / √2: A Deep Dive into Simplifying Radicals
Understanding how to simplify expressions involving radicals, like 4 / √2, is crucial in mathematics, particularly in algebra and calculus. This seemingly simple expression offers a gateway to mastering fundamental concepts of rationalizing denominators and simplifying surds. This article provides a comprehensive explanation of how to simplify 4 / √2, exploring various methods and delving into the underlying mathematical principles. We'll cover the steps involved, the rationale behind each step, and address frequently asked questions, ensuring a thorough understanding of this mathematical operation.
Understanding the Problem: 4 / √2
The expression 4 / √2 presents a challenge because it contains an irrational number in the denominator – the square root of 2 (√2). In mathematics, it's generally preferred to have rational numbers (numbers that can be expressed as a fraction of two integers) in the denominator. This process of eliminating the radical from the denominator is known as rationalizing the denominator.
Method 1: Rationalizing the Denominator
The most common and straightforward method for simplifying 4 / √2 involves multiplying both the numerator and the denominator by √2. This process leverages the property that multiplying a number by its square root results in the number itself (√a * √a = a).
Steps:
-
Multiply the numerator and denominator by √2:
(4 / √2) * (√2 / √2)
-
Simplify the numerator:
4 * √2 = 4√2
-
Simplify the denominator:
√2 * √2 = 2
-
Combine the simplified numerator and denominator:
4√2 / 2
-
Further Simplification:
Notice that both the numerator and denominator are divisible by 2. Dividing both by 2 gives:
2√2
Therefore, 4 / √2 simplifies to 2√2.
Method 2: Using the Properties of Radicals
We can also approach this simplification by utilizing the properties of radicals. Remember that the square root of a fraction is the square root of the numerator divided by the square root of the denominator: √(a/b) = √a / √b. We can apply this principle in reverse.
Steps:
-
Rewrite the expression as a single radical:
4 / √2 can be written as √(16/2) because 4 = √16.
-
Simplify the fraction inside the radical:
√(16/2) = √8
-
Simplify the radical:
√8 can be simplified further. Since 8 = 4 * 2, we get:
√8 = √(4 * 2) = √4 * √2 = 2√2
Thus, we again arrive at the simplified form: 2√2.
Method 3: A More Visual Approach
Imagine a square with a side length of √2 units. The area of this square is (√2)² = 2 square units. Now, consider a rectangle with an area four times the area of the square, meaning its area is 8 square units. If we maintain one side length of √2, the other side length must be 8/√2 = 4/√2. Through rationalizing the denominator (as shown in Method 1), we find that this other side length is 2√2. This visual representation offers an intuitive understanding of the simplification process.
The Significance of Rationalizing the Denominator
Rationalizing the denominator is important for several reasons:
- Easier Calculations: Working with rational numbers is generally simpler than working with irrational numbers. It makes subsequent calculations and comparisons significantly easier.
- Standardization: Rationalizing the denominator is a standard practice in mathematics, making it easier to compare and combine results.
- Avoidance of Ambiguity: Having irrational numbers in the denominator can sometimes lead to ambiguity in calculations, especially in more complex expressions.
Explaining the Result: 2√2
The simplified expression, 2√2, represents a precise numerical value. While it's not a whole number or a simple fraction, it’s a much cleaner and more manageable form than the original expression, 4/√2. The value of 2√2 is approximately 2.828. This demonstrates that simplifying the expression doesn't alter its fundamental numerical value, only its representation.
Approximating the Value
While the exact value of 2√2 is 2√2, we can find an approximate decimal value using a calculator:
2√2 ≈ 2.828427
This approximation is useful for practical applications where an exact value isn't strictly necessary.
Frequently Asked Questions (FAQs)
Q1: Why is it important to rationalize the denominator?
A1: Rationalizing the denominator makes calculations simpler and avoids potential ambiguity in more complex mathematical operations. It's also a standard practice that ensures consistency in mathematical presentations.
Q2: Can I use a calculator to directly solve 4/√2?
A2: Yes, a calculator can directly compute the decimal approximation of 4/√2. However, the goal of simplifying the expression is not just to find a numerical value but also to understand the underlying mathematical principles and obtain a more elegant and manageable representation.
Q3: Are there other methods to simplify expressions like this?
A3: While rationalizing the denominator is the most common and efficient method, other approaches might involve using different properties of radicals or factoring, depending on the specific expression. The chosen method will often depend on the context and the complexity of the expression.
Q4: What if the denominator was a more complex radical, say √(x+y)?
A4: Rationalizing the denominator for more complex radicals often requires multiplying by a conjugate (for example, multiplying by (√(x+y) + a) / (√(x+y) + a) for an appropriate value of a). The specific technique will depend on the structure of the radical expression.
Q5: Is the simplified form 2√2 an irrational number?
A5: Yes, 2√2 is still an irrational number. An irrational number is a number that cannot be expressed as a fraction of two integers. While we have simplified the expression, the presence of √2 maintains the irrational nature of the result.
Conclusion
Simplifying 4 / √2 to 2√2 is a fundamental skill in algebra. This article demonstrated three different methods for accomplishing this simplification, emphasizing the importance of rationalizing the denominator. Understanding these methods not only provides a practical skill but also strengthens one’s understanding of the fundamental properties of radicals and rational numbers. Remember, the process of simplification is as important as the final answer, offering insights into the elegance and efficiency of mathematical manipulation. Mastering this concept forms a strong foundation for more advanced mathematical explorations. The ability to manipulate and simplify radical expressions is crucial for success in higher-level math courses and for solving problems in various scientific and engineering fields.
Latest Posts
Latest Posts
-
Birds With 5 Letter Names
Sep 20, 2025
-
Many Litres In A Gallon
Sep 20, 2025
-
What Is 1 9 In Percentage
Sep 20, 2025
-
First Law Of Motion Images
Sep 20, 2025
-
How Long Is 33 Cm
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 4/ Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.