Lcm Of 4 And 13
seoindie
Sep 22, 2025 · 6 min read
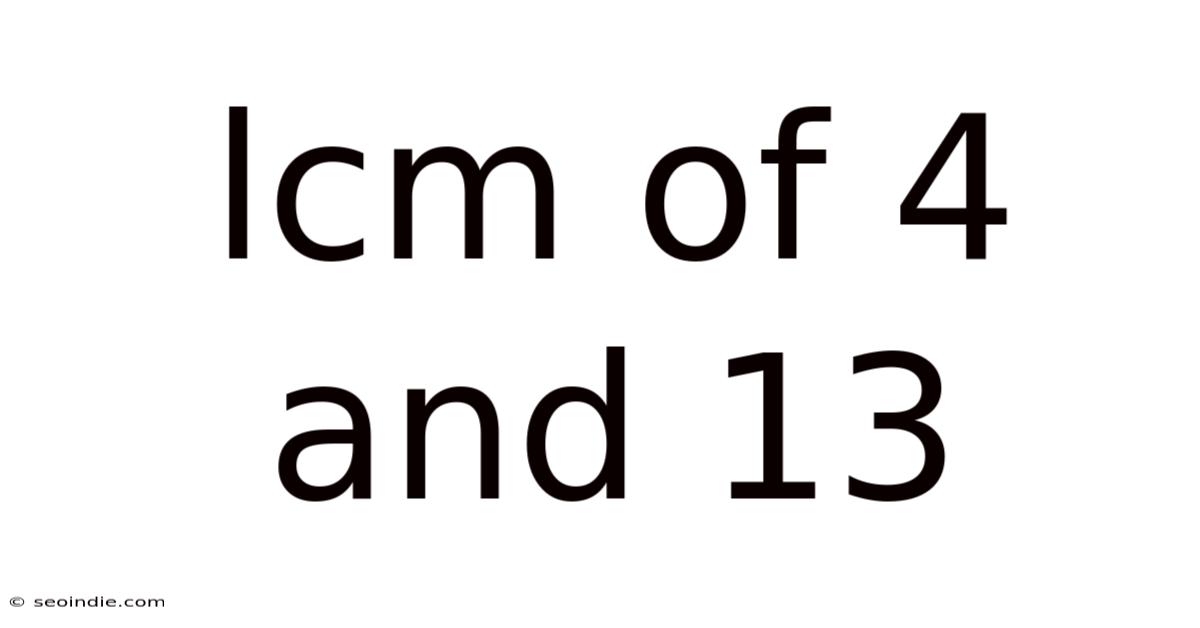
Table of Contents
Understanding the Least Common Multiple (LCM) of 4 and 13
Finding the least common multiple (LCM) might seem like a simple mathematical task, especially when dealing with smaller numbers like 4 and 13. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for building a strong foundation in mathematics. This article delves deep into finding the LCM of 4 and 13, exploring various approaches and explaining the theoretical underpinnings. We'll move beyond a simple answer to provide a comprehensive understanding of LCMs, their applications, and their significance in various mathematical contexts.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's a fundamental concept in number theory with applications ranging from simple fraction addition to complex scheduling problems. Understanding the LCM is vital for simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra.
Think of it this way: imagine you have two gears with different numbers of teeth. The LCM represents the smallest number of rotations each gear needs to complete before they both return to their starting positions simultaneously. This analogy helps visualize the concept of finding the smallest common multiple.
Methods for Calculating LCM
There are several methods to calculate the LCM, each with its own advantages and disadvantages. Let's explore the most common approaches, focusing on their application to find the LCM of 4 and 13.
1. Listing Multiples Method
This is the most straightforward approach, particularly suitable for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52,...
- Multiples of 13: 13, 26, 39, 52,...
By comparing the lists, we see that the smallest number present in both lists is 52. Therefore, the LCM of 4 and 13 is 52. This method is simple to visualize but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This approach is more efficient for larger numbers.
- Prime factorization of 4: 2²
- Prime factorization of 13: 13 (13 is a prime number)
To find the LCM using prime factorization:
- Identify all the prime factors present in either number. In this case, we have 2 and 13.
- For each prime factor, take the highest power that appears in any of the factorizations. The highest power of 2 is 2², and the highest power of 13 is 13¹.
- Multiply these highest powers together: 2² * 13 = 4 * 13 = 52.
Therefore, the LCM of 4 and 13 is 52. This method is generally more efficient than listing multiples, especially when dealing with larger numbers or numbers with many factors.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship provides another way to calculate the LCM.
First, we need to find the GCD of 4 and 13. The GCD is the largest positive integer that divides both numbers without leaving a remainder. In this case, the GCD(4, 13) = 1 because 1 is the only positive integer that divides both 4 and 13.
Now, we use the formula: LCM(a, b) = (a * b) / GCD(a, b)
LCM(4, 13) = (4 * 13) / 1 = 52
This method highlights the intimate connection between LCM and GCD, providing an alternative approach to calculating the LCM.
The Significance of LCM(4,13) = 52
The result, LCM(4, 13) = 52, has practical implications in various scenarios. For example:
- Fraction Addition/Subtraction: When adding or subtracting fractions with denominators 4 and 13, the LCM (52) becomes the least common denominator, simplifying the process.
- Cyclic Events: Imagine two events occurring cyclically. One event repeats every 4 units of time, and another every 13 units. The LCM (52) represents the smallest time interval after which both events occur simultaneously again.
- Modular Arithmetic: In modular arithmetic, the LCM plays a role in finding solutions to congruences.
While the numbers 4 and 13 might seem trivial, the process of finding their LCM illustrates fundamental concepts applicable to more complex problems.
Beyond the Basics: LCM and its Applications
The concept of LCM extends beyond simple integer calculations. It finds its application in numerous fields:
- Computer Science: In scheduling algorithms and resource management, determining the LCM helps optimize task execution and resource allocation.
- Music Theory: The LCM is used in determining the least common period of musical rhythms and melodies.
- Engineering: In designing systems with periodic components, such as gears or rotating shafts, the LCM helps ensure synchronized operation.
- Cryptography: In certain cryptographic algorithms, the LCM is involved in determining key lengths and periods.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers? How do I find the LCM?
A1: The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you consider all prime factors across all numbers and take the highest power of each. For the GCD method, you would need to iteratively apply the GCD and LCM calculations.
Q2: Is there a formula for the LCM of any two numbers?
A2: Yes, there's a direct formula relating LCM and GCD: LCM(a,b) = (a*b) / GCD(a,b). However, finding the GCD might still require an algorithm like the Euclidean algorithm.
Q3: Why is the LCM important in fraction arithmetic?
A3: The LCM is crucial because it provides the least common denominator (LCD) when adding or subtracting fractions. Using the LCD simplifies the process significantly and avoids unnecessary calculations.
Q4: Can the LCM of two numbers be smaller than the larger number?
A4: Yes. This occurs when one number is a multiple of the other. For example, LCM(2, 4) = 4.
Q5: Can the LCM of two numbers be equal to their product?
A5: Yes. This happens when the GCD of the two numbers is 1 (they are coprime or relatively prime). For instance, LCM(4, 13) = 4 * 13 because GCD(4, 13) = 1.
Conclusion
Finding the LCM of 4 and 13, while seemingly straightforward, serves as an excellent illustration of fundamental mathematical concepts. The various methods—listing multiples, prime factorization, and the GCD approach—each offer insights into different aspects of number theory. The LCM's applications extend far beyond simple arithmetic, playing a significant role in various fields, highlighting its practical importance and theoretical significance. Understanding LCM lays a solid foundation for tackling more complex mathematical problems and appreciating the interconnectedness of mathematical ideas. The seemingly simple calculation of LCM(4,13) = 52 unlocks a broader understanding of mathematical principles that are fundamental to problem-solving across diverse disciplines.
Latest Posts
Latest Posts
-
Is 361 A Perfect Square
Sep 22, 2025
-
All The Factors Of 85
Sep 22, 2025
-
5 Square Root Of 2
Sep 22, 2025
-
Words That Start With Tac
Sep 22, 2025
-
Words That Start With On
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.