Lcm Of 4 6 9
seoindie
Sep 13, 2025 · 6 min read
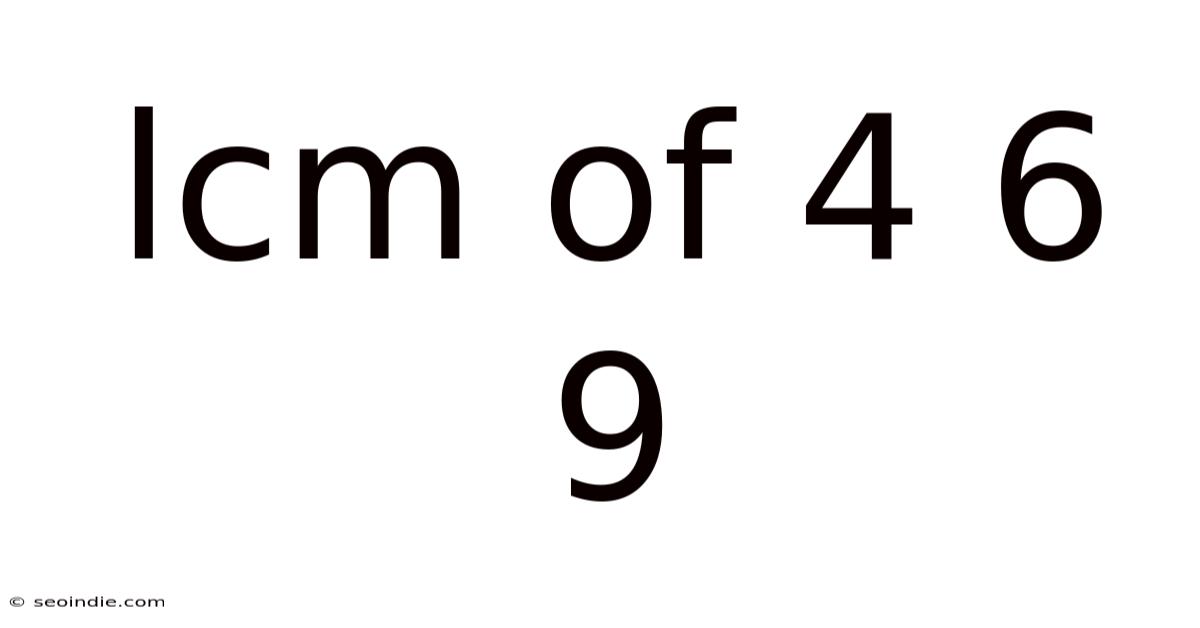
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex algebraic manipulations. This comprehensive guide will explore how to find the LCM of 4, 6, and 9, detailing various methods and offering a deeper understanding of the underlying principles. We'll also address common misconceptions and provide practical examples to solidify your understanding. This will equip you with the knowledge to confidently tackle similar problems involving LCM calculations.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what LCM means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer divisible by both 2 and 3.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 9: 9, 18, 27, 36, 45...
By inspecting the lists, we see that the smallest number appearing in all three lists is 36. Therefore, the LCM of 4, 6, and 9 is 36.
This method works well for smaller numbers, but it can become cumbersome and time-consuming for larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient and systematic, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Prime Factorization:
- 4 = 2²
- 6 = 2 × 3
- 9 = 3²
-
Constructing the LCM:
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
Therefore, the LCM is 2² × 3² = 4 × 9 = 36.
This method is significantly more efficient than listing multiples, especially for larger numbers. It provides a structured approach that is less prone to errors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are related through the following formula:
LCM(a, b) × GCD(a, b) = a × b
This formula can be extended to more than two numbers, although the calculation becomes more complex. While directly applying this formula to find the LCM of 4, 6, and 9 might seem less intuitive, understanding the relationship between LCM and GCD is crucial for a complete understanding of number theory. We will first find the GCD of 4, 6 and 9 using the Euclidean algorithm.
-
Finding the GCD: We can use the Euclidean algorithm to find the GCD of 4, 6, and 9. This involves finding the GCD of pairs of numbers repeatedly.
- GCD(4, 6) = 2 (because 4 = 2 x 2 and 6 = 2 x 3)
- GCD(2, 9) = 1
Therefore, the GCD of 4, 6, and 9 is 1.
- Using the LCM-GCD Relationship (for two numbers at a time): While the direct application of the LCM x GCD = a x b formula to three numbers requires a more intricate calculation, we can use it iteratively.
First, let's find the LCM of 4 and 6: LCM(4,6) x GCD(4,6) = 4 x 6 LCM(4,6) x 2 = 24 LCM(4,6) = 12
Now, let's find the LCM of 12 and 9: LCM(12,9) x GCD(12,9) = 12 x 9 LCM(12,9) x 3 = 108 LCM(12,9) = 36
Therefore, the LCM of 4, 6, and 9 is 36.
This method demonstrates the powerful relationship between LCM and GCD. Although more complex for multiple numbers, it offers a deeper insight into the mathematical connections between these concepts.
Method 4: Using the Least Common Multiple Calculator (Digital Tools)
Many online calculators and mathematical software packages offer LCM calculation tools. These tools can be particularly helpful for more complex scenarios involving many numbers or larger values. While convenient, it is important to understand the underlying principles to solve problems without reliance on digital tools, especially in situations without internet access or calculator availability.
Explanation of the Result: Why 36?
The LCM of 4, 6, and 9 is 36 because 36 is the smallest positive integer that is divisible by all three numbers without leaving a remainder. This is evident from the prime factorization method: 36 contains all the prime factors (2 and 3) raised to their highest powers found in the individual numbers (2² and 3²).
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder.
-
Q: Can the LCM of a set of numbers be one of the numbers in the set?
- A: Yes, this is possible if one number is a multiple of all the others. For example, the LCM of 2, 4, and 8 is 8.
-
Q: What if I have more than three numbers? How would I find the LCM?
- A: You can apply the prime factorization method or the iterative GCD method to find the LCM of any number of integers. For the prime factorization method, you simply include all prime factors raised to their highest power from all the numbers. For the iterative GCD method, you would find the LCM of two numbers, then the LCM of that result and the next number, and so on.
-
Q: Why is finding the LCM important?
- A: Finding the LCM is essential in various mathematical operations, such as:
- Adding or subtracting fractions: Finding the LCM of the denominators is crucial to create a common denominator.
- Solving problems involving cyclical events: Determining when events will occur simultaneously.
- Simplifying algebraic expressions: Finding common factors.
- A: Finding the LCM is essential in various mathematical operations, such as:
Conclusion
Finding the least common multiple (LCM) is a fundamental skill in mathematics with broad applications. This guide demonstrated various methods for calculating the LCM, including listing multiples, prime factorization, and using the relationship between LCM and GCD. While using a calculator is convenient, a thorough understanding of these methods is essential for developing a strong mathematical foundation and tackling more complex problems independently. The LCM of 4, 6, and 9, as shown through different methods, is definitively 36. Remember to choose the method best suited to the numbers involved and your level of comfort with different mathematical techniques. Remember to practice regularly to enhance your proficiency in LCM calculations.
Latest Posts
Latest Posts
-
3 Classes Of Levers Examples
Sep 13, 2025
-
Words With U And E
Sep 13, 2025
-
Aerobic Respiration Takes Place In
Sep 13, 2025
-
Lcm Of 8 And 30
Sep 13, 2025
-
Adj That Start With W
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 6 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.