Lcm Of 36 And 42
seoindie
Sep 16, 2025 · 6 min read
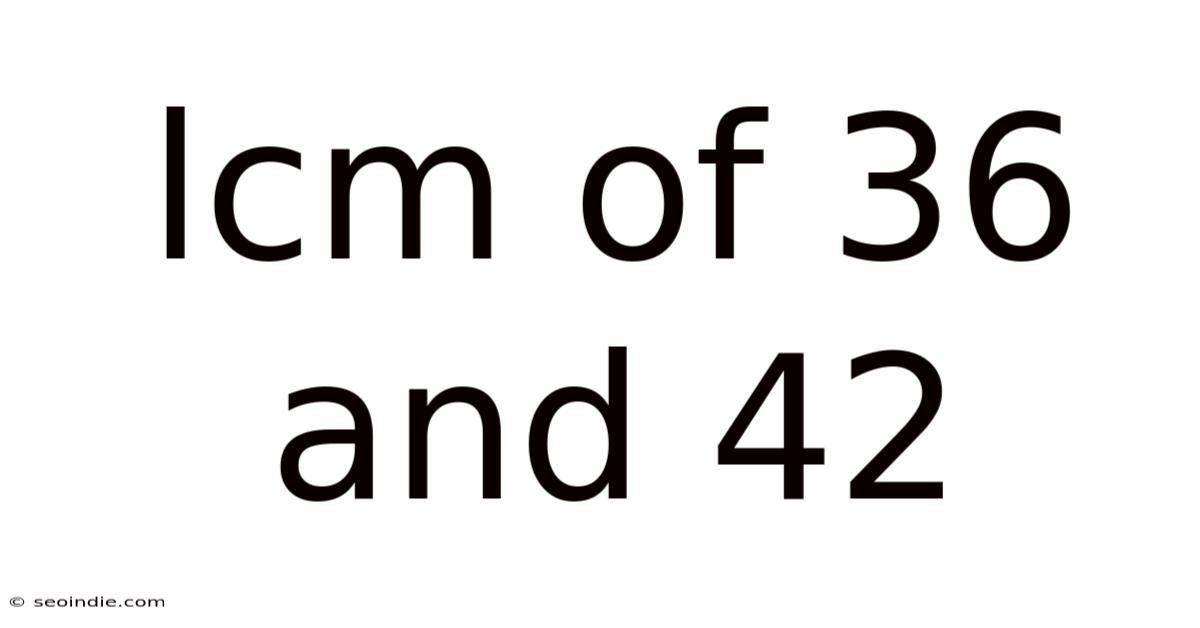
Table of Contents
Finding the Least Common Multiple (LCM) of 36 and 42: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it provides a valuable foundation in number theory and algebra. This comprehensive guide explores the LCM of 36 and 42, demonstrating multiple approaches, explaining the underlying mathematical principles, and addressing frequently asked questions. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems in algebra and beyond. Let's dive in!
Understanding Least Common Multiple (LCM)
Before we tackle the LCM of 36 and 42, let's establish a solid understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. For example, the multiples of 3 are 3, 6, 9, 12, 15… and the multiples of 4 are 4, 8, 12, 16, 20… The smallest number that appears in both lists is 12, therefore, the LCM of 3 and 4 is 12.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. Let's find the LCM of 36 and 42 using this approach:
First, we list the multiples of 36: 36, 72, 108, 144, 180, 216, 252…
Next, we list the multiples of 42: 42, 84, 126, 168, 210, 252…
By comparing the two lists, we find that the smallest number common to both is 252. Therefore, the LCM of 36 and 42 is 252.
While this method is simple and intuitive, it becomes less practical when dealing with larger numbers. Imagine trying to list the multiples of, say, 157 and 283!
Method 2: Prime Factorization
This method is more efficient and works well even with larger numbers. It relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Step 1: Find the prime factorization of each number.
- 36: 2 x 2 x 3 x 3 = 2² x 3²
- 42: 2 x 3 x 7
Step 2: Identify the highest power of each prime factor present in the factorizations.
In our example, the prime factors are 2, 3, and 7.
- The highest power of 2 is 2² (from 36).
- The highest power of 3 is 3² (from 36).
- The highest power of 7 is 7¹ (from 42).
Step 3: Multiply the highest powers together.
LCM(36, 42) = 2² x 3² x 7 = 4 x 9 x 7 = 252
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. It allows us to systematically find the LCM without needing to generate extensive lists.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that elegantly connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Step 1: Find the GCD of 36 and 42.
We can use the Euclidean algorithm to find the GCD:
- 42 = 36 x 1 + 6
- 36 = 6 x 6 + 0
The last non-zero remainder is 6, so GCD(36, 42) = 6.
Step 2: Apply the formula.
LCM(36, 42) = (36 x 42) / 6 = 1512 / 6 = 252
This method is also quite efficient, especially when the GCD can be easily calculated, for example, using the Euclidean Algorithm.
Mathematical Explanation and Properties of LCM
The concept of LCM is deeply rooted in number theory. Understanding its properties enhances our ability to apply it effectively in various mathematical contexts:
- Commutative Property: The order of the numbers doesn't affect the LCM. LCM(a, b) = LCM(b, a)
- Associative Property: When finding the LCM of more than two numbers, the grouping doesn't matter. LCM(a, LCM(b, c)) = LCM(LCM(a, b), c)
- Distributive Property with GCD: LCM(a, b) x GCD(a, b) = |a x b|
- Relationship with Fractions: The LCM is crucial in adding and subtracting fractions with different denominators. Finding the LCM of the denominators allows you to rewrite the fractions with a common denominator, facilitating the addition or subtraction.
Understanding these properties allows for more flexible and efficient approaches to solving problems involving LCMs.
Applications of LCM in Real-World Scenarios
While the concept might seem abstract, the LCM finds practical applications in numerous real-world scenarios:
- Scheduling: Imagine two buses that depart from the same station but on different schedules. Finding the LCM of their departure intervals helps determine when they'll both depart at the same time.
- Construction: In construction projects, the LCM can be used to synchronize different tasks with varying cycle times.
- Music: The LCM plays a role in understanding musical harmony and rhythm, helping determine when different musical patterns will align.
- Computer Science: LCM is applied in various algorithms and scheduling problems in computer science.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers? How do I find their LCM?
A: You can extend the prime factorization method or the GCD-based method. For prime factorization, find the prime factorization of each number, then take the highest power of each prime factor present. For the GCD method, you'd iteratively find the LCM of pairs of numbers.
Q: Is there a formula for the LCM of three or more numbers?
A: There isn't a single concise formula like the one for two numbers, but the prime factorization method readily extends to handle any number of integers.
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers evenly. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
Q: Can the LCM of two numbers be smaller than the larger of the two numbers?
A: Yes, this happens when one number is a multiple of the other. For example, LCM(4, 8) = 8.
Q: Can the LCM of two numbers be equal to their product?
A: Yes, this occurs when the two numbers are coprime (i.e., their GCD is 1). For example, LCM(6, 7) = 42 = 6 x 7.
Conclusion
Finding the least common multiple of 36 and 42, as demonstrated using three different methods, highlights the versatility and importance of this fundamental concept in number theory. Understanding the different approaches – listing multiples, prime factorization, and utilizing the GCD – equips you with various tools to tackle LCM problems efficiently, regardless of the numbers' size or complexity. The LCM is not merely an abstract mathematical concept; it holds practical applications in diverse fields, underscoring its significance in mathematics and beyond. By mastering the LCM, you build a stronger foundation for more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
How Many Feet Is 100meters
Sep 17, 2025
-
All The Factors Of 38
Sep 17, 2025
-
Sum Of 1 To 9
Sep 17, 2025
-
Are All Elements Pure Substances
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 36 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.