Sum Of 1 To 9
seoindie
Sep 17, 2025 · 6 min read
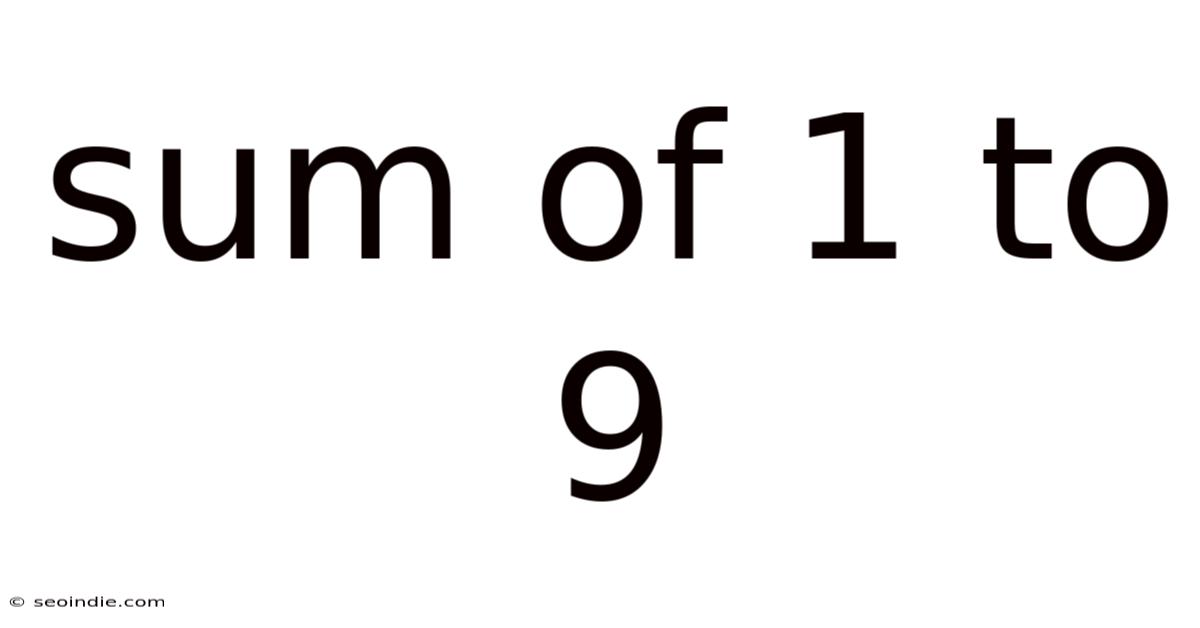
Table of Contents
Unlocking the Secrets of Summation: A Deep Dive into the Sum of 1 to 9
The seemingly simple question, "What is the sum of numbers from 1 to 9?", opens a door to a fascinating world of mathematical concepts, historical context, and practical applications. While the answer itself is easily calculated (45), the journey to understanding how to arrive at this answer and the broader implications of such calculations is far more enriching. This article delves into the sum of 1 to 9, exploring various methods of calculation, its connection to broader mathematical principles, and its relevance in various fields.
I. The Elementary Approach: Direct Addition
The most straightforward method to find the sum of numbers from 1 to 9 is simply adding them together: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. This approach is readily understandable, even for young learners, and serves as a solid foundation for understanding more complex summation techniques. It highlights the fundamental operation of addition and its role in arithmetic. However, this method becomes increasingly cumbersome as the range of numbers expands. Imagine trying to sum numbers from 1 to 1000 using this method! This is where more sophisticated techniques become necessary.
II. Gauss's Method: A Stroke of Genius
A far more elegant and efficient solution was famously devised by the young Carl Friedrich Gauss. Instead of adding the numbers sequentially, Gauss recognized a pattern. He paired the numbers from opposite ends of the sequence: 1 + 9 = 10, 2 + 8 = 10, 3 + 7 = 10, 4 + 6 = 10, leaving the number 5 in the middle. This resulted in four pairs summing to 10, plus the single number 5. The total sum is therefore (4 x 10) + 5 = 45.
This approach, while seemingly simple, showcases a fundamental principle of mathematical problem-solving: identifying patterns and exploiting symmetries. It’s far more efficient than direct addition, especially for larger ranges. This method can be generalized to find the sum of any arithmetic series.
III. The Formula for Arithmetic Series: Generalizing the Solution
Gauss's insight led to the development of a general formula for the sum of an arithmetic series. An arithmetic series is a sequence where the difference between consecutive terms remains constant (this constant is called the common difference). The sum of an arithmetic series can be calculated using the formula:
S = n/2 [2a + (n-1)d]
Where:
- S is the sum of the series
- n is the number of terms
- a is the first term
- d is the common difference
In our case, the sum of numbers from 1 to 9:
- n = 9 (there are nine terms)
- a = 1 (the first term is 1)
- d = 1 (the common difference is 1)
Plugging these values into the formula:
S = 9/2 [2(1) + (9-1)(1)] = 9/2 [2 + 8] = 9/2 (10) = 45
This formula provides a powerful and efficient way to calculate the sum of any arithmetic series, regardless of the size of the series. This is a crucial concept in various branches of mathematics, including calculus and statistics.
IV. Visual Representation: The Power of Geometry
The sum of 1 to 9 can also be visualized geometrically. Imagine arranging squares to form a rectangle. We can represent the sum 1+2+3+4+5+6+7+8+9 visually as a right-angled trapezoid. The number of squares in each row corresponds to the numbers 1 through 9. We can then rearrange these squares to form a rectangle with dimensions 9 x 5. The area of this rectangle, 45 square units, represents the sum. This geometric approach provides an intuitive understanding of the sum and highlights the connection between arithmetic and geometry. This visual method can be extremely helpful in explaining the concept to students who are visual learners.
V. Sigma Notation: A Concise Mathematical Language
Sigma notation (∑) provides a concise way to represent the sum of a series. The sum of numbers from 1 to 9 can be written as:
∑_(i=1)^9 i = 45
This notation means "the sum of i, where i starts at 1 and goes up to 9". Sigma notation is commonly used in higher-level mathematics to express complex sums and series efficiently and unambiguously. It's a crucial tool for understanding calculus and other advanced mathematical concepts.
VI. Applications in Real-World Scenarios
The seemingly simple sum of 1 to 9 has surprising real-world applications:
- Inventory Management: Imagine a small shop owner counting items in stock. If they have 9 different items, each with one unit, the total number of items is the sum of 1 to 9.
- Simple Statistics: Calculating the average of a small dataset involving consecutive numbers would utilize this sum.
- Programming: In computer programming, the sum of consecutive numbers frequently appears in loops and iterative processes, particularly in scenarios involving sequential data processing.
- Financial Calculations: Calculating simple interest over a period of 9 months with consistent payments would involve summing a series.
VII. Expanding the Scope: Sum of 1 to n
The techniques discussed above are not limited to the sum of 1 to 9. They can be generalized to calculate the sum of the first n natural numbers. The formula remains:
S = n(n+1)/2
This formula is exceptionally useful and provides a rapid method for calculating the sum of any number of consecutive integers starting from 1. This is a cornerstone of many mathematical proofs and algorithms.
VIII. Beyond the Basics: Exploring Related Concepts
Understanding the sum of 1 to 9 opens the door to exploring a plethora of related mathematical concepts:
- Arithmetic Progression: This forms the basis of understanding arithmetic sequences and series.
- Geometric Progression: While not directly related to the sum of 1 to 9 (which is an arithmetic progression), understanding geometric progression allows for the comparison and contrast of different types of series.
- Series and Sequences: The sum of 1 to 9 is a fundamental example within the broader study of series and sequences.
- Calculus: The concept of summation is essential to understanding calculus, specifically integration, which can be viewed as the summation of infinitely many infinitesimally small quantities.
IX. Frequently Asked Questions (FAQ)
-
Q: Is there a way to calculate the sum of 1 to 9 without using a formula?
- A: Yes, direct addition or Gauss's method are viable alternatives, though less efficient for larger numbers.
-
Q: What if the series doesn't start at 1?
- A: The formula needs adjustment. You would need to adapt the formula for arithmetic series, taking into account the starting value and the common difference.
-
Q: Can this be applied to negative numbers?
- A: Yes, the formula for arithmetic series can accommodate negative numbers as well. However, you must carefully consider the signs when applying the formula.
-
Q: What are the practical implications of understanding this concept?
- A: Understanding this concept is fundamental to many areas of mathematics, computer science, statistics, and finance. It lays a foundation for more advanced mathematical concepts.
X. Conclusion
The seemingly innocuous problem of summing the numbers from 1 to 9 unveils a wealth of mathematical principles and techniques. From the simple act of direct addition to the elegant formula for arithmetic series and its geometric representation, this exploration provides a foundational understanding of essential mathematical concepts. The journey from a basic arithmetic problem to a deeper appreciation of mathematical structure and its real-world applications is a testament to the power and beauty of mathematics. The seemingly simple answer, 45, represents far more than just a numerical value; it symbolizes the interconnectedness of mathematical ideas and their relevance in diverse fields. Mastering this foundational concept empowers one to tackle more complex mathematical challenges with confidence and ingenuity.
Latest Posts
Latest Posts
-
Infinite Line Charge Electric Field
Sep 17, 2025
-
Is 0 001 Less Than 0 05
Sep 17, 2025
-
How Many Inches Is 70cm
Sep 17, 2025
-
5000 M2 To Sq Ft
Sep 17, 2025
-
Moment Of Inertia And Torque
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Sum Of 1 To 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.