Lcm Of 3 And 11
seoindie
Sep 20, 2025 · 6 min read
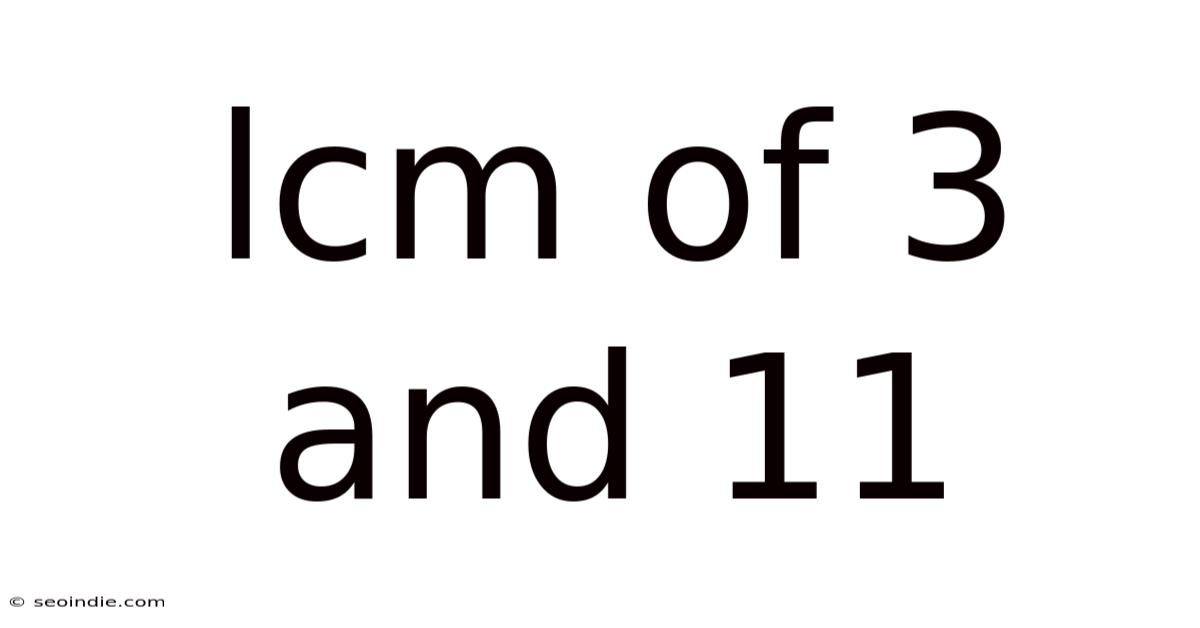
Table of Contents
Unveiling the Least Common Multiple (LCM) of 3 and 11: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating glimpse into number theory. This article delves into the LCM of 3 and 11, explaining not just the calculation but also the broader mathematical principles at play. We'll explore various methods for finding the LCM, discuss its applications, and address frequently asked questions. This comprehensive guide will equip you with a solid understanding of LCMs and their significance in mathematics.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific case of 3 and 11, let's establish a firm grasp on the concept of the LCM. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be evenly divided by each of the given integers without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers like 3 and 11 is to list their multiples until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36...
- Multiples of 11: 11, 22, 33, 44, 55, 66...
By inspecting the lists, we can see that the smallest number appearing in both lists is 33. Therefore, the LCM of 3 and 11 is 33.
This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers. For larger numbers, more sophisticated methods are necessary.
Method 2: Prime Factorization
A more powerful and efficient method for finding the LCM, especially for larger numbers, involves prime factorization. This method relies on expressing each number as a product of its prime factors. Prime factors are prime numbers that when multiplied together, produce the original number.
Let's apply this to 3 and 11:
- Prime factorization of 3: 3 (3 is a prime number itself)
- Prime factorization of 11: 11 (11 is also a prime number)
To find the LCM using prime factorization, we follow these steps:
- Identify the prime factors: We've already done this: 3 and 11.
- Find the highest power of each prime factor: Since both 3 and 11 appear only once in their respective factorizations, the highest power of each is simply 3¹ and 11¹.
- Multiply the highest powers together: LCM(3, 11) = 3¹ * 11¹ = 33
This method is more systematic and efficient than listing multiples, especially when dealing with larger numbers with multiple prime factors.
Method 3: Using the Formula LCM(a, b) = (|a * b|) / GCD(a, b)
Another efficient approach involves using the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a well-known relationship between the LCM and GCD:
LCM(a, b) = (|a * b|) / GCD(a, b)
where |a * b| represents the absolute value of the product of a and b.
Let's apply this to 3 and 11:
- Find the GCD of 3 and 11: Since 3 and 11 are both prime numbers and have no common factors other than 1, their GCD is 1.
- Apply the formula: LCM(3, 11) = (3 * 11) / 1 = 33
This formula provides a concise and efficient way to calculate the LCM, especially when the GCD is easily determined.
The Significance of LCM in Real-World Applications
The concept of LCM isn't just a theoretical exercise; it finds practical applications in various fields:
- Scheduling: Imagine two buses that arrive at a bus stop at different intervals. One bus arrives every 3 minutes, and the other every 11 minutes. The LCM (33 minutes) tells us when both buses will arrive at the stop simultaneously.
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
- Cyclic events: In physics and engineering, LCMs are used to determine when cyclical events align or repeat simultaneously. This has applications in wave interference, gear ratios, and other periodic phenomena.
- Project management: In project management, LCM helps in determining the synchronization points of different tasks with different durations.
Further Exploration: Extending LCM to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, we simply consider all prime factors and their highest powers across all the numbers. For the GCD-based formula, it's slightly more complex, requiring iterative application of the GCD calculation.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The least common multiple (LCM) is the smallest number that is a multiple of all given numbers. The greatest common divisor (GCD) is the largest number that divides all given numbers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases.
Q2: Can the LCM of two numbers be smaller than the larger of the two numbers?
A2: No. The LCM is always greater than or equal to the larger of the two numbers.
Q3: Is there a shortcut to finding the LCM of two numbers if one is a multiple of the other?
A3: Yes, if one number is a multiple of the other, the larger number is the LCM. For example, LCM(2, 4) = 4.
Q4: How do I find the LCM of three or more numbers?
A4: You can use either the prime factorization method or an iterative approach using the GCD method. For prime factorization, find the prime factorization of each number and take the highest power of each prime factor present in any of the factorizations. For the iterative GCD method, find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
Conclusion: Mastering the LCM
Understanding the least common multiple is fundamental to various areas of mathematics and its applications. While finding the LCM of 3 and 11 might seem trivial, the underlying principles and methods are widely applicable. By mastering these methods – listing multiples, prime factorization, and the GCD-based formula – you'll develop a strong foundation in number theory and be well-equipped to tackle more complex mathematical problems. Remember that the best method depends on the specific numbers involved; for small numbers, listing multiples might suffice, while for larger numbers, prime factorization or the GCD-based formula is more efficient. The key is understanding the underlying concepts and choosing the appropriate method for optimal efficiency.
Latest Posts
Latest Posts
-
Convert 80 Kilometers To Miles
Sep 20, 2025
-
Dorsal Side Of A Frog
Sep 20, 2025
-
Words Using The Suffix Able
Sep 20, 2025
-
Convert 20 Lbs To Kilos
Sep 20, 2025
-
Difference Between Capacitor And Battery
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.