Lcm Of 24 And 21
seoindie
Sep 22, 2025 · 6 min read
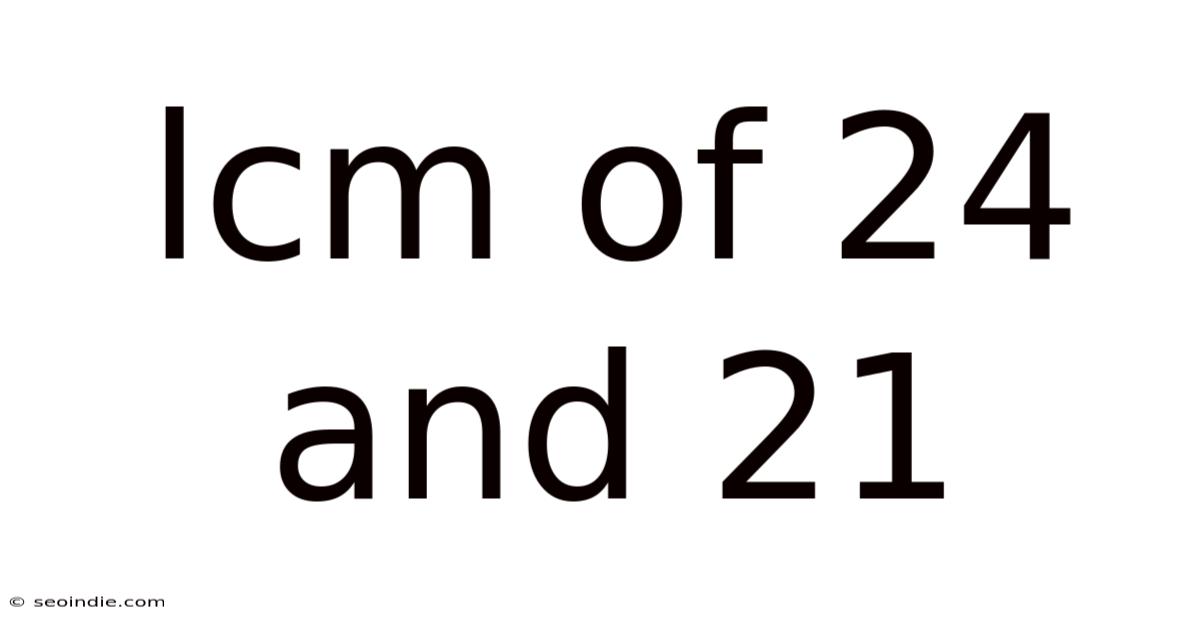
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 21: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple mathematical task, especially when dealing with smaller numbers like 24 and 21. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for building a strong foundation in mathematics. This article will delve deep into finding the LCM of 24 and 21, exploring various methods, explaining the underlying principles, and addressing common questions. We'll move beyond a simple answer and equip you with the knowledge to tackle more complex LCM problems.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly. This concept is fundamental in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra.
Understanding the LCM is essential for various practical applications. For instance, if you have two gears rotating at different speeds, represented by their number of rotations per minute, the LCM helps determine when both gears will be at the same position simultaneously. Similarly, in scheduling events that repeat at different intervals, the LCM helps determine when those events will coincide.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 24 and 21, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240, 264, 288, 312, 336...
- Multiples of 21: 21, 42, 63, 84, 105, 126, 147, 168, 189, 210, 231, 252, 273, 294...
By comparing the two lists, we see that the smallest number appearing in both lists is 168. Therefore, the LCM of 24 and 21 is 168. This method is simple to understand but can become inefficient and time-consuming when dealing with larger numbers.
Method 2: Prime Factorization
This method offers a more efficient and systematic approach, particularly for larger numbers. It involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves.
-
Prime Factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
-
Prime Factorization of 21: 21 = 3 x 7 = 3¹ x 7¹
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together.
In this case, the prime factors are 2, 3, and 7. The highest power of 2 is 2³ (from 24), the highest power of 3 is 3¹ (both numbers have 3¹), and the highest power of 7 is 7¹ (from 21).
Therefore, LCM(24, 21) = 2³ x 3¹ x 7¹ = 8 x 3 x 7 = 168.
This method is far more efficient than listing multiples, especially when dealing with larger numbers or finding the LCM of multiple numbers. It provides a structured approach and eliminates the need for extensive listing.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Finding the GCD of 24 and 21: We can use the Euclidean algorithm to find the GCD.
- 24 = 21 x 1 + 3
- 21 = 3 x 7 + 0
The last non-zero remainder is 3, so GCD(24, 21) = 3.
-
Calculating the LCM: Now, we can use the formula:
LCM(24, 21) = (24 x 21) / 3 = 504 / 3 = 168.
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging. The Euclidean algorithm provides an efficient way to determine the GCD, which then allows for a quick calculation of the LCM.
Explanation of the Mathematical Principles
The methods above rely on fundamental concepts of number theory. Prime factorization is based on the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This unique representation is the key to the efficiency of the prime factorization method for finding the LCM.
The relationship between the LCM and GCD is a consequence of the properties of divisibility and the prime factorization of integers. The formula LCM(a, b) = (|a x b|) / GCD(a, b) elegantly captures this relationship, offering an alternative and often more efficient way to compute the LCM.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest multiple common to both numbers, while the GCD is the largest divisor common to both numbers. They are inversely related, as shown by the formula connecting them.
-
Can I use a calculator to find the LCM? Many calculators have built-in functions for calculating the LCM and GCD. However, understanding the underlying methods is crucial for problem-solving and deeper mathematical understanding.
-
Why is finding the LCM important? The LCM has practical applications in various fields, including scheduling, gear ratios, and simplifying fractions. It ensures that we find the smallest common denominator when working with fractions, making calculations easier and more manageable.
-
What if I have more than two numbers? The methods described (prime factorization in particular) can be extended to find the LCM of more than two numbers. You would find the prime factorization of each number and then take the highest power of each prime factor present in any of the factorizations.
Conclusion: Mastering LCM Calculations
Finding the least common multiple of 24 and 21, as we've demonstrated, can be approached through several methods. While the simple listing of multiples works for smaller numbers, prime factorization and the GCD method provide more efficient and systematic approaches for handling larger numbers and more complex problems. Understanding the mathematical principles behind these methods is essential for building a solid mathematical foundation. Mastering LCM calculations not only improves your mathematical skills but also equips you with a powerful tool for solving various real-world problems. Remember, the most important aspect is not just getting the answer (168 in this case) but understanding why that answer is correct and being able to apply these techniques to a wider range of problems. Practice is key to mastering these concepts and gaining confidence in your mathematical abilities. Don't be afraid to experiment with different methods and choose the one that suits your understanding and the specific problem at hand.
Latest Posts
Latest Posts
-
Relationship Between Energy And Wavelength
Sep 22, 2025
-
Is 5 6 A Natural Number
Sep 22, 2025
-
Indian States And State Animals
Sep 22, 2025
-
Flowers Blowing In The Wind
Sep 22, 2025
-
Things To Write About Myself
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.