Lcm Of 2 5 6
seoindie
Sep 24, 2025 · 6 min read
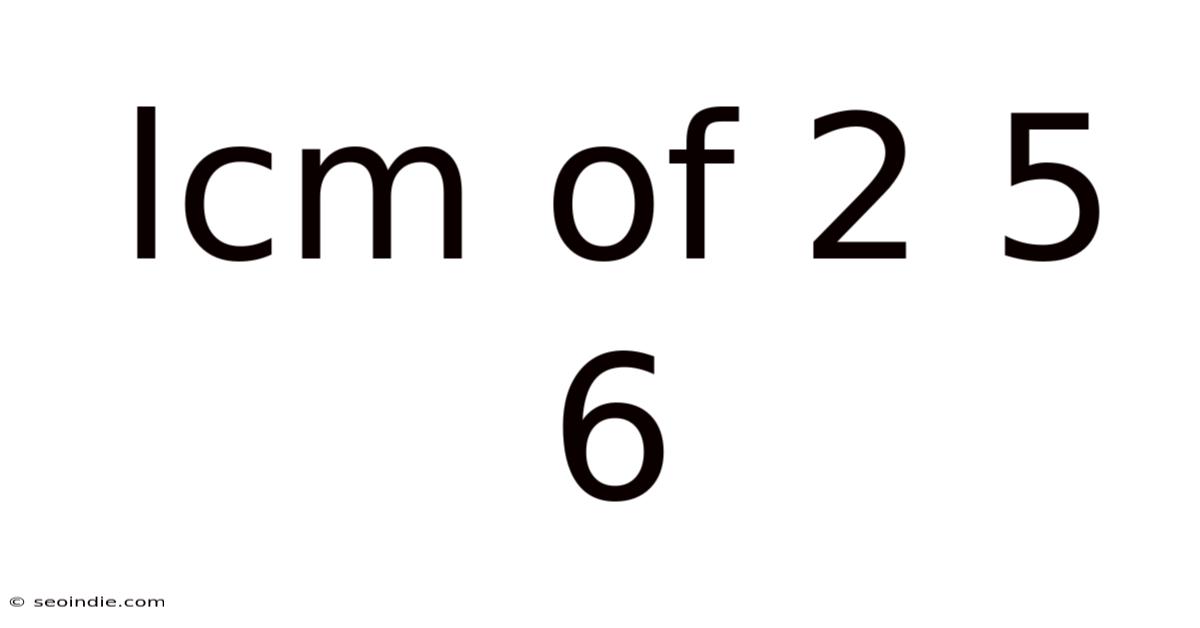
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving problems in algebra and beyond. This article provides a detailed explanation of how to calculate the LCM of 2, 5, and 6, exploring different methods and delving into the underlying mathematical principles. We'll also address common misconceptions and frequently asked questions to ensure a complete understanding of this essential mathematical skill.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) is the smallest positive integer that is a multiple of all the integers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number that is divisible by both 2 and 3. Understanding LCM is crucial for tasks such as adding or subtracting fractions with different denominators, and many other mathematical operations. This article will specifically focus on finding the LCM of 2, 5, and 6, illustrating multiple methods to achieve this.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By inspecting the lists, we see that the smallest number appearing in all three lists is 30. Therefore, the LCM of 2, 5, and 6 is 30. This method is simple but can become tedious for larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It relies on expressing each number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
-
Prime Factorization:
- 2 = 2¹
- 5 = 5¹
- 6 = 2¹ × 3¹
-
Identifying the Highest Power of Each Prime Factor: We look at each prime factor that appears in the factorizations (2, 3, and 5) and choose the highest power of each.
- The highest power of 2 is 2¹.
- The highest power of 3 is 3¹.
- The highest power of 5 is 5¹.
-
Multiplying the Highest Powers: We multiply these highest powers together to find the LCM. LCM(2, 5, 6) = 2¹ × 3¹ × 5¹ = 2 × 3 × 5 = 30
Therefore, the LCM of 2, 5, and 6 is 30 using the prime factorization method. This method is more systematic and less prone to error, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
While this formula is directly applicable to two numbers, we can extend it to multiple numbers by applying it iteratively.
First, let's find the GCD of 2 and 5 using the Euclidean algorithm:
- Divide 5 by 2: 5 = 2 × 2 + 1
- Divide 2 by 1: 2 = 1 × 2 + 0
The GCD(2, 5) = 1.
Now, let's find the LCM(2, 5) using the formula:
LCM(2,5) × GCD(2,5) = 2 × 5 LCM(2,5) × 1 = 10 LCM(2,5) = 10
Next, let's find the GCD of 10 and 6:
- Divide 10 by 6: 10 = 6 × 1 + 4
- Divide 6 by 4: 6 = 4 × 1 + 2
- Divide 4 by 2: 4 = 2 × 2 + 0
The GCD(10, 6) = 2.
Now, let's find the LCM(10, 6) using the formula:
LCM(10,6) × GCD(10,6) = 10 × 6 LCM(10,6) × 2 = 60 LCM(10,6) = 30
Therefore, the LCM of 2, 5, and 6 is 30 using this iterative GCD method. This method, although more complex than prime factorization for this specific example, demonstrates a powerful relationship between LCM and GCD and is particularly useful in more advanced mathematical contexts.
Mathematical Explanation: Why This Works
The prime factorization method works because it ensures that we capture all the prime factors present in the numbers, each raised to their highest power. By doing so, we guarantee that the resulting number is divisible by each of the original numbers. The LCM is the smallest such number, hence its importance. The iterative GCD method leverages the inherent relationship between the LCM and GCD, providing an alternative approach to finding the LCM.
Applications of LCM
Understanding and calculating LCM has widespread applications across various mathematical fields and real-world scenarios. Here are some examples:
- Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
- Scheduling: Determining when events will occur simultaneously. For example, if one event happens every 2 days, another every 5 days, and a third every 6 days, the LCM will tell us when all three events will coincide.
- Modular Arithmetic: LCM plays a crucial role in modular arithmetic, used in cryptography and other areas of computer science.
- Music: In music theory, LCM is used to determine the least common denominator for rhythms and time signatures.
Frequently Asked Questions (FAQ)
- What if the numbers have common factors? The prime factorization method easily handles numbers with common factors. The common factors will be included only once in the LCM, raised to their highest power.
- Can I use this method for more than three numbers? Yes, absolutely! Both the prime factorization and iterative GCD methods can be extended to any number of integers. For prime factorization, simply include all prime factors from all the numbers, choosing the highest power of each. For the iterative GCD method, apply it iteratively, finding the LCM of two numbers at a time.
- Is there a formula for the LCM of three or more numbers? There isn't a single, direct formula like the one for two numbers. However, the methods described (prime factorization and iterative GCD) provide systematic ways to calculate the LCM for any number of integers.
- Why is the LCM important? The LCM is crucial because it represents the smallest common multiple, allowing for efficient solutions in various mathematical problems, especially those involving fractions, cycles, and scheduling.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with many practical applications. We've explored three distinct methods – listing multiples, prime factorization, and the iterative GCD approach – to calculate the LCM of 2, 5, and 6, all yielding the answer 30. The prime factorization method offers a more efficient and systematic approach, especially for larger numbers, while the iterative GCD method highlights the close relationship between LCM and GCD. Mastering these methods will empower you to tackle more complex mathematical problems and gain a deeper understanding of number theory. Remember to practice regularly to build your proficiency in this essential mathematical concept.
Latest Posts
Latest Posts
-
Words That Start With Lau
Sep 24, 2025
-
X 4 X 5 2
Sep 24, 2025
-
Cubic Foot To Cubic Inches
Sep 24, 2025
-
Convert 12 5 Inches To Cm
Sep 24, 2025
-
Proof Of Isosceles Triangle Theorem
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.