X 4 X 5 2
seoindie
Sep 24, 2025 · 6 min read
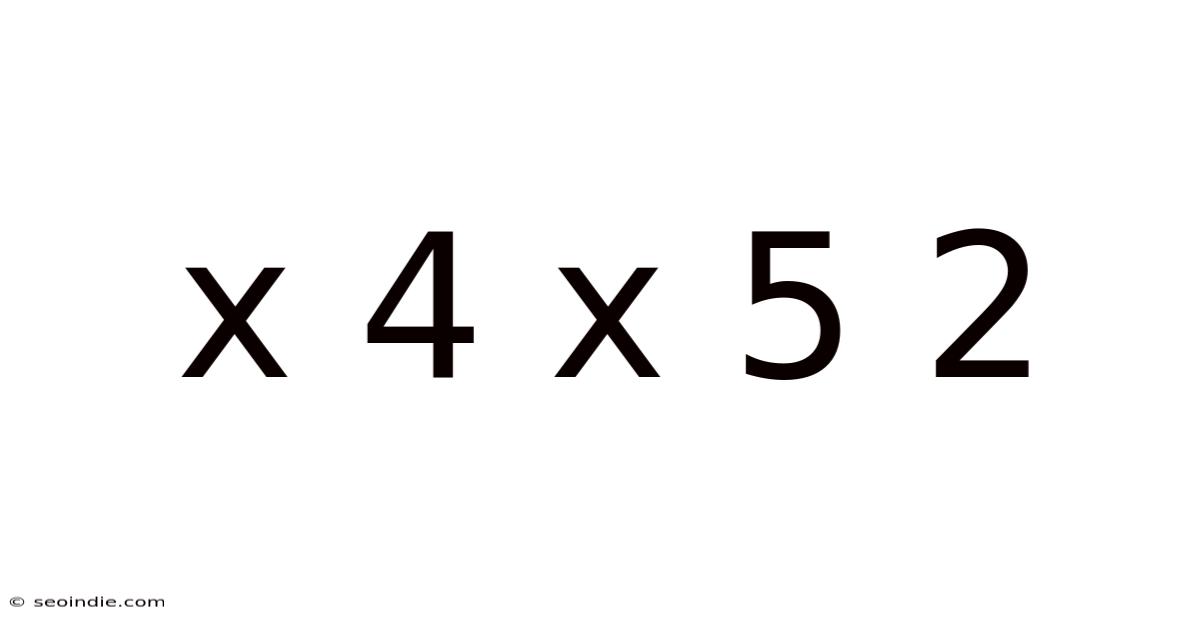
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x 4 x 5 2"
This article delves into the mathematical expression "x 4 x 5 2," exploring its various interpretations, potential ambiguities, and the importance of precise mathematical notation. We will uncover how different understandings of operator precedence and the use of implied multiplication can lead to vastly different results. Understanding this seemingly simple expression highlights the critical need for clarity and consistency in mathematical communication. This exploration will be beneficial for students, educators, and anyone interested in the nuances of mathematical language.
Understanding Operator Precedence: The PEMDAS/BODMAS Rule
The core of interpreting "x 4 x 5 2" lies in understanding operator precedence. This is the order in which mathematical operations are performed. The widely used acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) represent this order. Both acronyms essentially convey the same rules, with slight variations in terminology.
- Parentheses/Brackets: Operations within parentheses or brackets are always performed first.
- Exponents/Orders: Exponents (powers or indices) are calculated next.
- Multiplication and Division: These operations have equal precedence and are performed from left to right.
- Addition and Subtraction: These operations also have equal precedence and are performed from left to right.
The absence of parentheses or exponents in "x 4 x 5 2" simplifies the problem, focusing our attention on the order of multiplication.
Interpreting "x 4 x 5 2": Potential Interpretations and Ambiguity
The ambiguity in "x 4 x 5 2" stems from the lack of explicit multiplication symbols and the potential for implied multiplication. Let's consider different interpretations:
Interpretation 1: Strictly Left-to-Right Multiplication
If we interpret the expression strictly from left to right, assuming all instances of juxtaposition represent multiplication, we would calculate as follows:
(x * 4) * 5 * 2 = 40x
This interpretation treats each "x" as a separate variable and applies the multiplication sequentially.
Interpretation 2: Implied Multiplication and Grouping
Another interpretation involves considering implied multiplication, where the juxtaposition of a number and a variable, or two numbers, suggests multiplication without an explicit symbol. This leads to different groupings:
- Grouping 1: x(4 x 5 x 2) = 40x
This interpretation groups the numbers 4, 5, and 2 together before multiplying by x.
- Grouping 2: (x 4)(5 2) = 20x
This interpretation involves grouping "x 4" and "5 2" separately, and multiplying these groups together. This implies that "x 4" is treated as a single entity. This is far less common interpretation because it involves implying grouping based on visual proximity that isn’t standard mathematical practice.
- Grouping 3: x(4)(5)(2) = 40x
Here, each number is treated as a separate factor multiplied by x, yielding the same result as Interpretation 1 and Grouping 1.
The Importance of Clear Mathematical Notation
The multiple interpretations highlighted above demonstrate the importance of using clear and unambiguous mathematical notation. The expression "x 4 x 5 2" is inherently ambiguous because it relies on implied multiplication and lacks explicit grouping symbols. This ambiguity can lead to errors and misunderstandings, especially in more complex mathematical contexts.
To avoid ambiguity, one should always use explicit multiplication symbols (*) and parentheses ( ) to clearly indicate the order of operations. For instance, the expression could be rewritten in several unambiguous ways:
- Option 1 (Left-to-right): (x * 4) * 5 * 2 = 40x
- Option 2 (Grouping numbers): x * (4 * 5 * 2) = 40x
- Option 3 (Alternative Grouping): (x * 4) * (5 * 2) = 40x
These options eliminate any uncertainty about the intended order of operations.
Extending the Concept: Incorporating Exponents and Variables
Let's explore a slightly more complex scenario incorporating exponents and multiple variables. Consider the expression: x² 4 y 5 z 2
Without clear notation, this expression is also highly ambiguous. However, we can explore potential interpretations, assuming, as before, that juxtaposition implies multiplication:
-
Interpretation A: Left-to-right Multiplication: (x² * 4) * y * 5 * z * 2 = 40x²yz
-
Interpretation B: Grouping Numerical Coefficients: x² * (4 * 5 * 2) * y * z = 40x²yz
Again, we see that different interpretations based on implied multiplication result in the same outcome.
The ambiguity in this scenario highlights even more strongly the need for careful use of mathematical notation, including parentheses, to eliminate any doubt about the intended calculation. For example, a clearer version of this expression could be: (x²) * 4 * y * (5 * z) * 2 = 40x²yz
Practical Implications and Real-World Examples
The issue of ambiguous mathematical notation isn't just a theoretical concern; it has real-world implications, particularly in programming and scientific calculations. Programming languages often have strict rules regarding operator precedence, but even then, the lack of clear notation in the initial expression can lead to unexpected results.
For example, if a programmer were to input "x 4 x 5 2" into a program, the output could vary depending on the programming language's handling of implied multiplication and operator precedence. This could lead to errors in scientific simulations, financial models, or any other application requiring precise mathematical computations.
In scientific literature or engineering documents, ambiguous notation can result in misinterpretations of equations or formulas, leading to potentially serious consequences. Therefore, maintaining clarity and using explicit notation is vital for accuracy and reliability.
Frequently Asked Questions (FAQ)
Q: Is there a universally accepted interpretation for "x 4 x 5 2"?
A: No, there isn't. The lack of explicit multiplication symbols and parentheses creates ambiguity, leading to different interpretations depending on how implied multiplication is handled.
Q: Why is using explicit multiplication symbols and parentheses so important?
A: Explicit notation eliminates ambiguity and ensures that the intended order of operations is clear, reducing the risk of errors and misunderstandings. It also improves the readability and understandability of mathematical expressions.
Q: Can implied multiplication ever be used without causing confusion?
A: While implied multiplication is sometimes used in concise mathematical notation, it's generally advisable to avoid it in situations where clarity is paramount. Using explicit symbols significantly reduces the risk of misinterpretation.
Q: Are there any specific mathematical conventions that address this type of ambiguity?
A: While there aren't specific conventions addressing this exact type of ambiguous expression, general mathematical conventions emphasize the importance of clear and unambiguous notation. Using parentheses to group terms and explicit multiplication symbols is strongly recommended.
Conclusion
The seemingly simple expression "x 4 x 5 2" reveals the critical importance of precise mathematical notation. The potential for multiple interpretations highlights the necessity of using explicit multiplication symbols (*) and parentheses ( ) to eliminate ambiguity and ensure accurate calculations. This understanding is not just a matter of academic interest but also crucial in programming, scientific work, and any field relying on accurate mathematical computations. By emphasizing clear notation, we can prevent misunderstandings and ensure the reliability of mathematical expressions in all contexts. The consistent and clear application of operator precedence rules (PEMDAS/BODMAS) combined with explicit mathematical notation guarantees accurate results and avoids the potential pitfalls associated with implied multiplication and ambiguous expressions. Remember, precision in mathematical communication is paramount.
Latest Posts
Latest Posts
-
How To Calculate Linear Speed
Sep 24, 2025
-
Is 512 A Perfect Square
Sep 24, 2025
-
Difference Between Purine And Pyrimidine
Sep 24, 2025
-
Is Calcium Hydroxide A Base
Sep 24, 2025
-
10 Examples Of Exclamatory Sentence
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.