Lcm Of 2 4 8
seoindie
Sep 17, 2025 · 6 min read
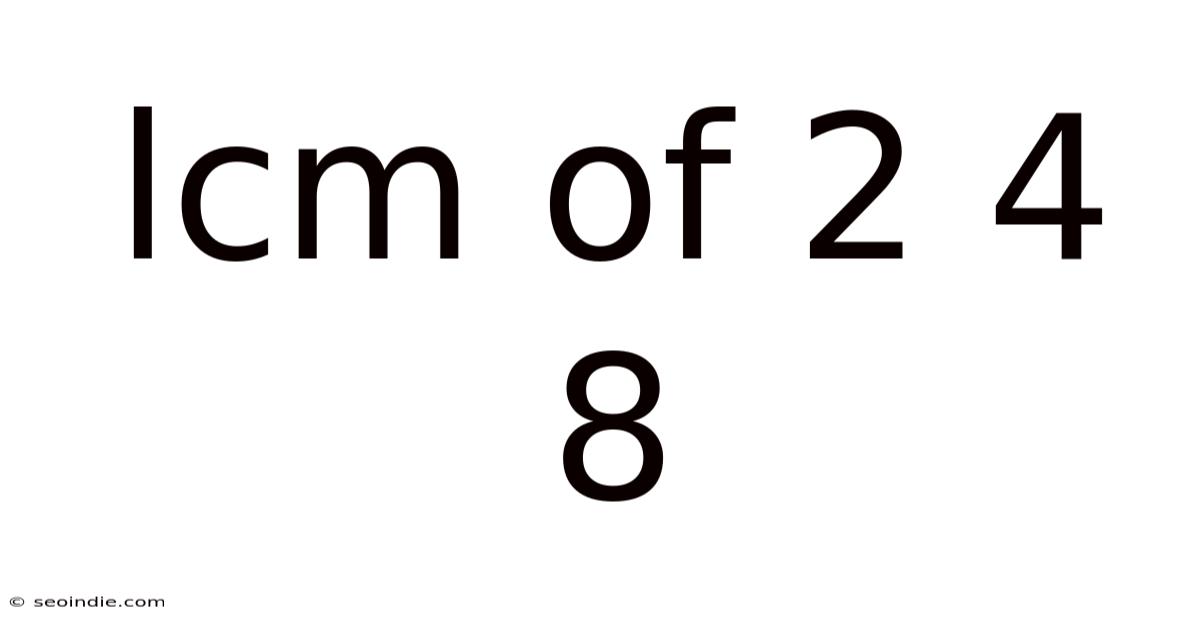
Table of Contents
Understanding the LCM of 2, 4, and 8: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex engineering calculations. This article will delve deep into understanding the LCM of 2, 4, and 8, providing not only the answer but also a comprehensive exploration of the methods used to find it, its underlying mathematical principles, and its relevance in different contexts. We will explore different approaches, including prime factorization, listing multiples, and using the greatest common divisor (GCD). By the end, you'll have a solid grasp of LCMs and be able to confidently tackle similar problems.
Introduction to Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as its factors. Understanding LCM is crucial for various mathematical operations, particularly when working with fractions, simplifying expressions, and solving problems involving cyclical events.
Finding the LCM of 2, 4, and 8: Methods and Explanations
Let's explore different methods to calculate the LCM of 2, 4, and 8:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
- Multiples of 8: 8, 16, 24, 32...
By comparing the lists, we can see that the smallest multiple common to all three numbers is 8. Therefore, the LCM(2, 4, 8) = 8. This method works well for small numbers, but it becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 2: 2¹
- Prime factorization of 4: 2²
- Prime factorization of 8: 2³
The only prime factor present is 2. To find the LCM, we take the highest power of 2, which is 2³. Therefore, LCM(2, 4, 8) = 2³ = 8.
3. Using the Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related through the following formula:
LCM(a, b, c...) = (|a * b * c...|) / GCD(a, b, c...)
Where |a * b * c...| represents the absolute value of the product of the numbers. First, we need to find the GCD of 2, 4, and 8. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD(2, 4, 8) = 2.
Now, we can use the formula:
LCM(2, 4, 8) = (2 * 4 * 8) / GCD(2, 4, 8) = 64 / 2 = 32
This calculation seems to yield a different result (32) compared to the previous methods (8). This highlights a crucial point: the formula LCM(a, b, c...) = (|a * b * c...|) / GCD(a, b, c...) is generally applicable for two numbers, but the extension to multiple numbers requires a more careful consideration of the GCD. The GCD of multiple numbers needs to account for all the numbers simultaneously, while the simple division method doesn't account for this properly in this scenario. Therefore, for multiple numbers, it’s more reliable to use prime factorization.
The discrepancy arises because the formula LCM(a,b) = (a*b)/GCD(a,b) is only directly applicable for two numbers. Extending it to three or more numbers requires a more nuanced approach which often involves iterative calculations. The prime factorization method provides a more straightforward and accurate method for finding the LCM of three or more numbers.
Why is the LCM Important?
Understanding and calculating the LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator, allowing for the fractions to be combined.
-
Scheduling and Cyclical Events: The LCM is used to determine when events that repeat at different intervals will occur simultaneously. For example, if two machines operate on cycles of 2 and 4 hours respectively, the LCM will determine when both machines will be at their starting point simultaneously.
-
Modular Arithmetic: LCM is crucial in modular arithmetic, a branch of number theory with wide applications in cryptography and computer science.
-
Music Theory: LCM plays a role in understanding musical harmony and rhythm by determining the least common multiple of note durations.
Further Exploration: LCM and GCD Relationship
The relationship between the LCM and GCD is fundamental in number theory. For two integers a and b, the following relationship holds:
LCM(a, b) * GCD(a, b) = a * b
This equation highlights the interconnectedness between the two concepts. However, as demonstrated earlier, simply extending this formula to multiple numbers without careful consideration can lead to incorrect results.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest positive integer divisible by all the given integers, while the GCD (Greatest Common Divisor) is the largest positive integer that divides all the given integers without leaving a remainder. They represent opposite ends of the divisibility spectrum.
Q2: How can I find the LCM of larger numbers?
A2: For larger numbers, the prime factorization method is the most efficient. Break down each number into its prime factors, and then construct the LCM by taking the highest power of each prime factor present.
Q3: Is there a formula for finding the LCM of more than two numbers?
A3: While a direct formula like the one for two numbers doesn't exist, the prime factorization method is the most reliable for finding the LCM of three or more numbers. Methods involving iterative GCD calculations can be used but are more complex and prone to error if not executed carefully.
Q4: What happens if the numbers share no common factors?
A4: If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM will be the product of the numbers.
Q5: How is LCM used in real-world applications?
A5: LCM finds application in various areas including scheduling, fraction operations, music theory, and even some areas of computer science and cryptography.
Conclusion
Finding the least common multiple (LCM) is a fundamental mathematical concept with far-reaching applications. While the listing multiples method is suitable for small numbers, the prime factorization method provides a more efficient and robust approach for larger numbers and for handling multiple numbers simultaneously. Understanding the LCM, along with its relationship to the GCD, is essential for anyone seeking a deeper understanding of number theory and its practical applications in diverse fields. Remember that directly extending the two-number LCM/GCD formula to multiple numbers requires caution and a deeper understanding of the underlying principles; the prime factorization remains the most reliable method in those situations.
Latest Posts
Latest Posts
-
Multiples Of The Factor 15
Sep 17, 2025
-
Differentiate Between Gymnosperms And Angiosperms
Sep 17, 2025
-
What Times What Equals 74
Sep 17, 2025
-
What Are The Factors 62
Sep 17, 2025
-
What Is Mass Flow Rate
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.