What Times What Equals 74
seoindie
Sep 17, 2025 · 6 min read
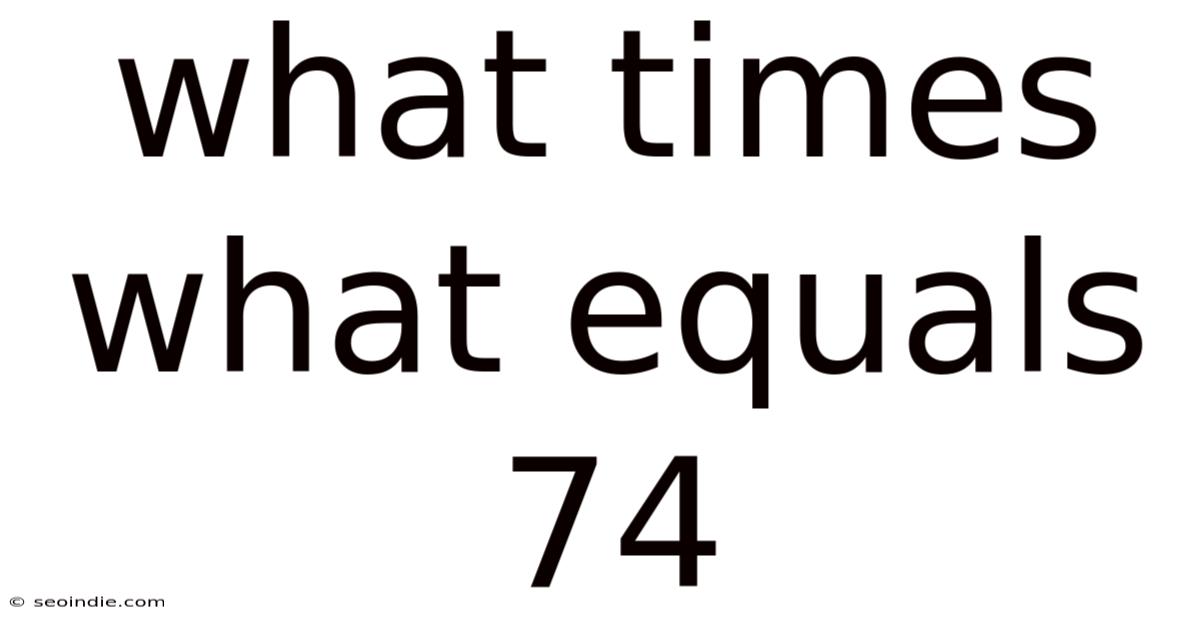
Table of Contents
Decoding the Mystery: What Times What Equals 74? A Deep Dive into Factorization
Finding the factors of a number might seem like a simple arithmetic problem, especially for a number like 74. But beneath the surface lies a fascinating world of mathematical concepts, from prime factorization to the broader implications of number theory. This article will not only answer the question "What times what equals 74?" but also explore the underlying principles and offer a deeper understanding of factorization.
Introduction: Understanding Factors and Factorization
Before diving into the specifics of 74, let's establish a foundational understanding of factors. Factors are whole numbers that divide evenly into a given number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Factorization, then, is the process of breaking down a number into its factors. This process is crucial in various mathematical operations, from simplifying fractions to solving algebraic equations.
Finding the Factors of 74: A Step-by-Step Approach
The simplest way to find the factors of 74 is through systematic trial and error. We start by checking the smallest whole numbers:
- 1: 74 is divisible by 1 (74 x 1 = 74).
- 2: 74 is divisible by 2 (37 x 2 = 74).
- 37: 74 is divisible by 37 (2 x 37 = 74).
We can stop here because we've already found the pair (2, 37). Any further attempts to find factors will simply repeat these numbers in reverse order (37 x 2 = 74, etc.). Therefore, the answer to "What times what equals 74?" is 2 multiplied by 37.
Prime Factorization: Unveiling the Building Blocks
The factorization we've just completed isn't just a simple breakdown; it's also the prime factorization of 74. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Prime numbers are the fundamental building blocks of all other whole numbers. In the case of 74, its prime factorization is 2 x 37, where both 2 and 37 are prime numbers.
The concept of prime factorization is not only important for understanding the structure of numbers but also plays a significant role in more advanced mathematical concepts such as cryptography and data compression. Unique prime factorization means that every whole number (excluding 1) can be expressed as a product of primes in only one way, regardless of the order of the factors.
Beyond the Basics: Exploring Related Mathematical Concepts
The seemingly simple question of finding factors of 74 opens doors to a wealth of mathematical concepts. Let's delve into a few:
-
Greatest Common Divisor (GCD): The GCD of two or more numbers is the largest number that divides all of them without leaving a remainder. For example, if we wanted to find the GCD of 74 and another number, say 98, we would find the prime factorization of both numbers and identify the common factors. The highest power of the common factor would be the GCD.
-
Least Common Multiple (LCM): The LCM is the smallest positive number that is a multiple of two or more numbers. Just as the GCD helps to simplify fractions, the LCM is crucial when adding or subtracting fractions with different denominators. Finding the LCM involves similar techniques to finding the GCD, utilizing prime factorization.
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. For example, in modulo 5 arithmetic, 74 would be equivalent to 4 (74 divided by 5 leaves a remainder of 4). This seemingly abstract concept has practical applications in cryptography, computer science, and even music theory.
-
Divisibility Rules: Understanding divisibility rules is a shortcut to quickly check if a number is divisible by a smaller number without performing long division. For example, a number is divisible by 2 if it's even; divisible by 3 if the sum of its digits is divisible by 3; and divisible by 5 if it ends in 0 or 5. Knowing these rules can significantly speed up the process of finding factors.
Applications of Factorization: Real-World Examples
Factorization isn't confined to the realm of theoretical mathematics; it has practical applications in various fields:
-
Cryptography: Public-key cryptography, which secures online transactions, heavily relies on the difficulty of factoring very large numbers into their prime factors. The strength of many encryption algorithms rests on this computational challenge.
-
Computer Science: Factorization algorithms are used in computer science for tasks like data compression and code optimization. Efficient factorization techniques can improve the performance of various computer programs.
-
Engineering: Engineers use factorization in structural design calculations and signal processing. Understanding the factors of specific numbers is critical for efficient design and problem-solving in these fields.
Frequently Asked Questions (FAQ)
Q: Are there other ways to find the factors of 74 besides trial and error?
A: Yes, there are more sophisticated methods for finding factors, especially for larger numbers. These include algorithms like the sieve of Eratosthenes and more advanced factorization techniques used in computer science. However, for smaller numbers like 74, trial and error is often the most efficient approach.
Q: What if the number is very large? How do I find its factors?
A: For larger numbers, trial and error becomes impractical. Sophisticated algorithms are needed, and often, even the most powerful computers struggle to factor extremely large numbers quickly. This is the basis of the security of many cryptographic systems.
Q: Is prime factorization unique for every number?
A: Yes, the Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This is a cornerstone of number theory.
Q: Why is prime factorization important?
A: Prime factorization is fundamental to number theory and has broad applications in cryptography, computer science, and various other fields. Understanding the prime factors of a number provides insights into its properties and enables efficient problem-solving in diverse contexts.
Conclusion: A Deeper Appreciation for the Simple Question
The seemingly simple question, "What times what equals 74?", has led us on a journey through the fascinating world of factorization and number theory. We've not only answered the initial question (2 x 37) but also explored the deeper mathematical principles underpinning this simple arithmetic operation. From prime numbers to the implications for cryptography, the exploration has shown the profound impact of this elementary concept on advanced mathematical fields and real-world applications. It's a reminder that even the most basic mathematical problems can hold surprising depth and complexity, offering opportunities for continued learning and exploration. The journey of understanding numbers is an endless one, full of intriguing discoveries waiting to be unearthed.
Latest Posts
Latest Posts
-
Difference In Area And Perimeter
Sep 17, 2025
-
What Does A Commutator Do
Sep 17, 2025
-
Differentiate Micro And Macro Economics
Sep 17, 2025
-
Greatest Common Factor For 72
Sep 17, 2025
-
Limits And Derivatives Class 11
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 74 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.