Lcm Of 18 And 3
seoindie
Sep 12, 2025 · 6 min read
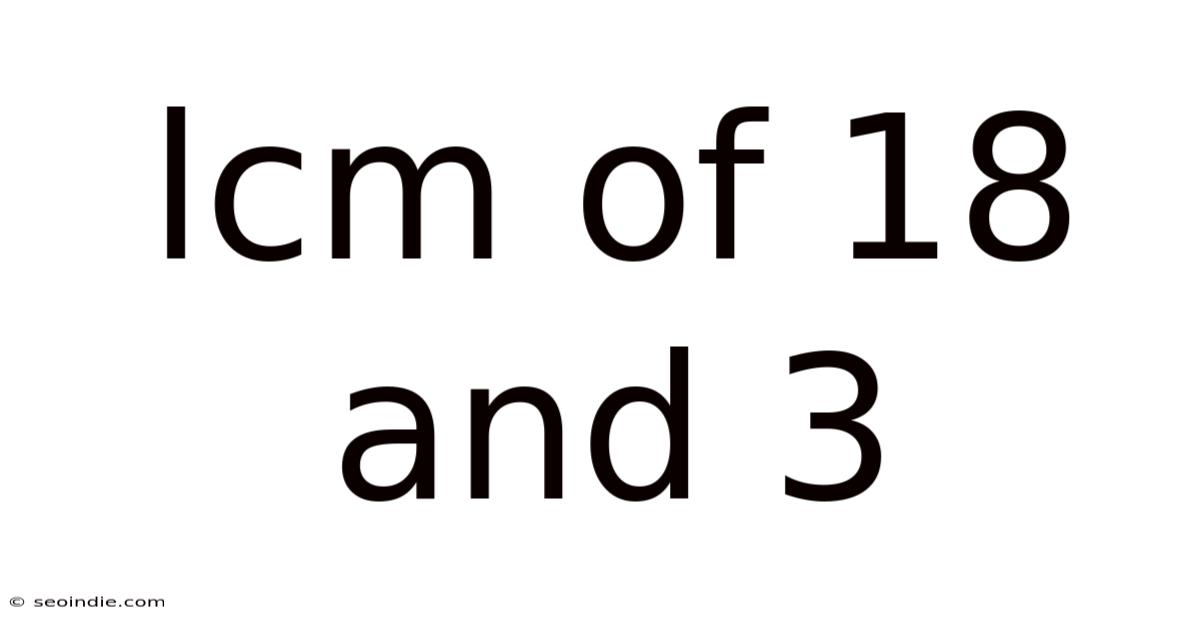
Table of Contents
Unveiling the Least Common Multiple (LCM) of 18 and 3: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, especially when dealing with smaller numbers like 18 and 3. However, understanding the underlying principles behind LCM calculations is crucial for grasping more complex mathematical concepts in algebra, calculus, and beyond. This comprehensive guide will not only show you how to find the LCM of 18 and 3 but also explore the theoretical foundations, different methods of calculation, and practical applications of this important concept. We'll even delve into some frequently asked questions to ensure a complete understanding.
Understanding Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. This concept extends to more than two numbers as well. Understanding LCM is vital in various mathematical operations, including simplifying fractions, solving equations, and working with rhythmic patterns in music.
Methods for Finding the LCM of 18 and 3
Several methods can be used to calculate the LCM. Let's explore the most common ones, applying them to find the LCM of 18 and 3.
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, ...
By comparing the lists, we can see that the smallest multiple common to both is 18. Therefore, the LCM of 18 and 3 is 18.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 3: 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹
- Highest power of 3: 3²
Multiplying these together gives us 2 x 3² = 2 x 9 = 18. Therefore, the LCM of 18 and 3 is 18.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD (Greatest Common Divisor). The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This can be expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 18 and 3 using the Euclidean algorithm or prime factorization.
- Prime factorization of 18: 2 x 3²
- Prime factorization of 3: 3
The common prime factor is 3, and the lowest power is 3¹. Therefore, the GCD(18, 3) = 3.
Now, we can use the formula:
LCM(18, 3) x GCD(18, 3) = 18 x 3
LCM(18, 3) x 3 = 54
LCM(18, 3) = 54 / 3 = 18
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method is particularly insightful because it reveals the fundamental building blocks of the numbers involved. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In essence, prime numbers are divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely expressed as a product of prime numbers. This unique factorization is crucial in various mathematical fields.
Understanding prime factorization helps us appreciate the structure of numbers and their relationships. When we find the LCM using prime factorization, we're essentially identifying the minimum set of prime factors needed to encompass both numbers. This approach extends easily to finding the LCM of more than two numbers. For instance, to find the LCM of 18, 3, and 6, we would factorize each number (18 = 2 x 3², 3 = 3, 6 = 2 x 3) and then select the highest power of each prime factor present (2¹ and 3²), giving us an LCM of 2 x 9 = 18.
Applications of LCM in Real-World Scenarios
While finding the LCM of 18 and 3 might seem abstract, the concept has practical applications in various areas:
-
Scheduling: Imagine two buses departing from a station at different intervals. One bus departs every 18 minutes, and the other departs every 3 minutes. The LCM (18) tells us when both buses will depart simultaneously again – every 18 minutes.
-
Fractions: Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators.
-
Pattern Recognition: In music, LCM helps determine when rhythmic patterns repeat simultaneously.
-
Project Management: LCM can be used to coordinate tasks with varying completion times, optimizing schedules and resource allocation.
-
Construction and Engineering: Calculating the LCM is crucial in tasks involving the precise measurement and alignment of materials, ensuring proper synchronization of processes.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The Least Common Multiple (LCM) is the smallest number divisible by both (or all) given numbers. The Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF), is the largest number that divides both (or all) given numbers without leaving a remainder. They are inversely related; knowing one helps find the other using the formula mentioned earlier.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, as demonstrated with the LCM of 18 and 3, where the LCM (18) is one of the original numbers. This happens when one number is a multiple of the other.
Q: How do I find the LCM of more than two numbers?
A: The prime factorization method works best for this. Factorize each number into its prime factors. Then, identify the highest power of each prime factor present across all the numbers and multiply them together to get the LCM.
Q: Is there a formula for LCM?
A: There isn't a single, universally applicable formula like there is for addition or subtraction. The methods outlined earlier (listing multiples, prime factorization, GCD method) are the standard approaches. However, the relationship between LCM and GCD, LCM(a,b) * GCD(a,b) = a*b, provides an indirect formula.
Conclusion
Finding the LCM of 18 and 3, while seemingly simple, opens the door to understanding a fundamental concept in number theory with extensive practical applications. Mastering the various methods for calculating LCM, particularly the prime factorization method, provides a solid foundation for tackling more complex mathematical problems. The exploration of prime numbers and their significance in factorization adds another layer to appreciating the structure and beauty of mathematics. From scheduling tasks to simplifying fractions, the LCM plays a vital role in numerous areas, showcasing the practical relevance of seemingly abstract mathematical concepts. Hopefully, this in-depth exploration has not only provided the answer but also illuminated the broader significance of the LCM within the vast landscape of mathematics.
Latest Posts
Latest Posts
-
3 7 To A Percent
Sep 12, 2025
-
Number Of Protons In Xenon
Sep 12, 2025
-
Difference Between Css And Scss
Sep 12, 2025
-
Chain Rule And Product Rule
Sep 12, 2025
-
4 Letter Words Starting D
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 18 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.