3 7 To A Percent
seoindie
Sep 12, 2025 · 5 min read
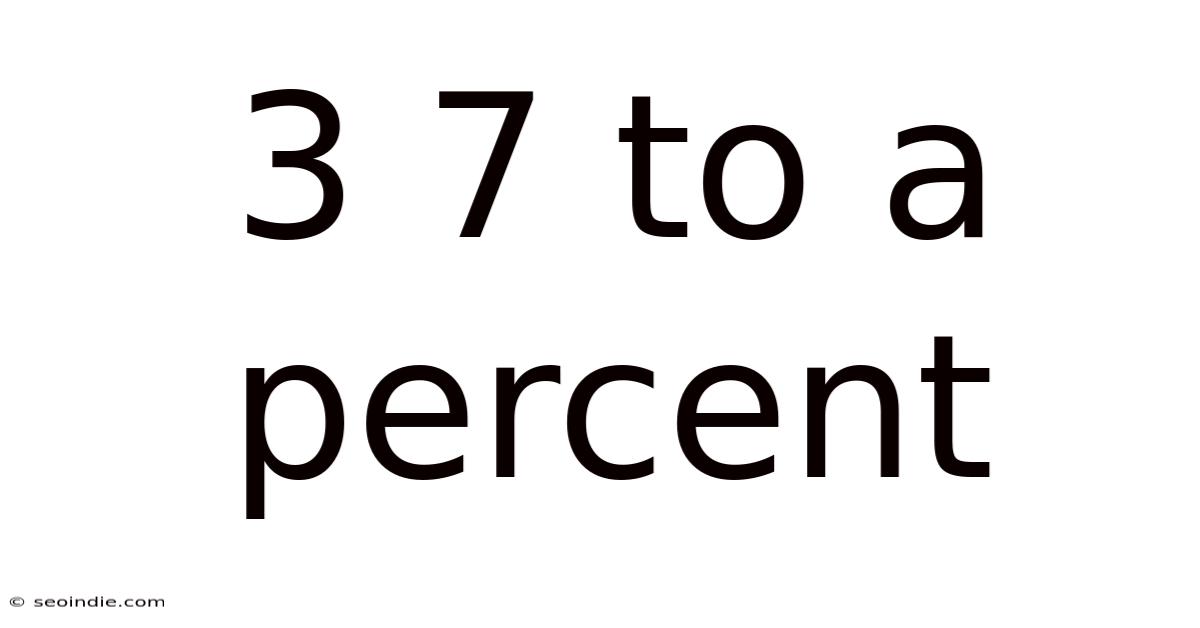
Table of Contents
Decoding the Mystery: Converting 3/7 to a Percentage
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will walk you through the process of converting the fraction 3/7 to a percentage, explaining the underlying principles and providing you with the tools to tackle similar conversions confidently. We'll explore different methods, ensuring you grasp the concepts fully, regardless of your mathematical background. By the end, you'll not only know the percentage equivalent of 3/7 but also understand the logic behind the conversion, making you proficient in tackling future fraction-to-percentage problems.
Understanding Fractions and Percentages
Before diving into the conversion, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 3/7, 3 is the numerator and 7 is the denominator. This means we're considering 3 parts out of a total of 7 equal parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion as a part of a hundred. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. The key to converting fractions to percentages is to find the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using Division
The most straightforward method to convert 3/7 to a percentage is by performing division. We divide the numerator (3) by the denominator (7):
3 ÷ 7 ≈ 0.42857
This decimal result represents the fractional value of 3/7. To convert this decimal to a percentage, we simply multiply by 100:
0.42857 × 100 ≈ 42.857%
Therefore, 3/7 is approximately equal to 42.86% when rounded to two decimal places. This method is simple and efficient for most fraction-to-percentage conversions.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves manipulating the fraction to find an equivalent fraction with a denominator of 100. However, in the case of 3/7, finding a whole number multiplier to achieve a denominator of 100 is not directly possible. 7 does not divide evenly into 100. This highlights a limitation of this method for fractions with denominators that aren't factors of 100. While conceptually straightforward, it’s practically less convenient for this specific fraction.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We set up a proportion:
3/7 = x/100
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
7x = 300
x = 300/7
x ≈ 42.857
Multiplying by 100 to express this as a percentage gives us approximately 42.86%. This method offers a more algebraic approach to solving the problem and reinforces the concept of proportional relationships.
Understanding the Approximation
It's crucial to acknowledge that the percentage we've calculated (42.86%) is an approximation. The decimal representation of 3/7 (0.42857142857...) is a non-terminating, repeating decimal. Rounding to two decimal places provides a practical and commonly used level of accuracy, but it's important to remember that the true value is slightly different. Depending on the context, you may need to use more decimal places for greater accuracy. For most practical purposes, 42.86% offers sufficient precision.
Illustrative Examples: Real-world Applications
Let's consider some real-world scenarios where understanding the conversion of 3/7 to a percentage is valuable:
-
Grade Calculation: Imagine a student scored 3 out of 7 points on a quiz. Converting 3/7 to a percentage (approximately 42.86%) provides a clearer understanding of their performance relative to the total possible points.
-
Sales Commission: If a salesperson earns a commission based on a fraction of sales, converting the fraction to a percentage makes it easier to calculate the actual commission amount. For example, if their commission is 3/7 of total sales, knowing it's roughly 42.86% simplifies the calculation.
-
Survey Results: In a survey where 3 out of 7 respondents answered "yes" to a question, converting the fraction to a percentage (approximately 42.86%) helps in summarizing and presenting the results effectively.
-
Recipe Scaling: If a recipe calls for 3/7 of a cup of an ingredient, converting this to a percentage can help in scaling the recipe up or down easily. For example, knowing it's about 43% of a cup makes it simpler to adjust the quantity based on the desired scale.
Frequently Asked Questions (FAQ)
Q1: Why is the decimal representation of 3/7 non-terminating and repeating?
A1: This is because the denominator (7) does not contain only factors of 2 and 5. Decimal representations terminate only when the denominator contains only factors of 2 and/or 5 (or can be reduced to a fraction with such a denominator). Since the prime factorization of 7 is simply 7, its decimal representation will repeat indefinitely.
Q2: Can I use a calculator for this conversion?
A2: Absolutely! Calculators are efficient tools for performing the division and multiplication steps involved in converting fractions to percentages.
Q3: Is rounding always necessary?
A3: Rounding is often necessary when dealing with non-terminating decimals, like the one obtained from dividing 3 by 7. The level of rounding depends on the required precision for the specific application. In many cases, rounding to two decimal places (as we did here) is sufficient.
Q4: Are there other ways to represent 3/7 besides a percentage?
A4: Yes, you can represent 3/7 as a decimal (approximately 0.4286) or as a ratio (3:7). The choice of representation depends on the context and the desired level of detail.
Conclusion
Converting 3/7 to a percentage involves a simple yet crucial mathematical process. We've explored three methods—direct division, attempting equivalent fractions (which proved less efficient here), and using proportions—highlighting the flexibility and applicability of different mathematical approaches. Understanding the underlying principles, alongside the practical applications showcased, empowers you to confidently tackle similar conversions and apply this knowledge across various fields. Remember, while we approximated the answer as 42.86%, it’s vital to acknowledge the ongoing, repeating nature of the decimal form for a complete mathematical understanding. Mastering fraction-to-percentage conversions is a valuable skill that enhances your mathematical proficiency and problem-solving abilities.
Latest Posts
Latest Posts
-
10 3 As A Decimal
Sep 12, 2025
-
What Are The Factors 37
Sep 12, 2025
-
Electric Field Of Spherical Shell
Sep 12, 2025
-
Mixed Number To Decimal Converter
Sep 12, 2025
-
Adj That Start With D
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 7 To A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.