Lcm For 8 And 9
seoindie
Sep 21, 2025 · 6 min read
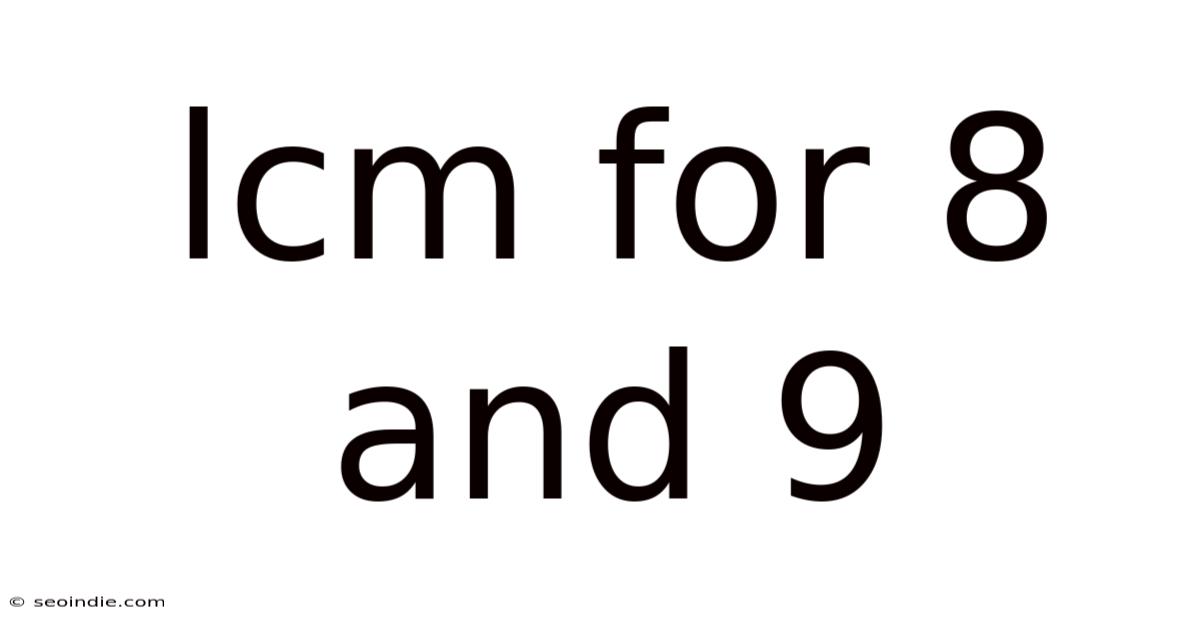
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts is crucial for grasping more advanced mathematical concepts. This comprehensive guide will delve into calculating the LCM of 8 and 9, explaining multiple methods, exploring the theoretical background, and answering frequently asked questions. We'll also look at the applications of LCMs in various fields. This guide is perfect for students learning about LCMs, teachers needing supplementary material, or anyone interested in refreshing their mathematical knowledge. Understanding LCMs is fundamental to working with fractions, solving problems involving cyclical events, and even understanding musical rhythms.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 8 and 9, let's define the term. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of both (or all) the numbers you're considering. For example, the multiples of 2 are 2, 4, 6, 8, 10… and the multiples of 3 are 3, 6, 9, 12… The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 8 and 9. Let's list the multiples of each number:
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80…
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81…
By comparing the two lists, we can see that the smallest number common to both is 72. Therefore, the LCM of 8 and 9 is 72.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(8, 9) = 2³ x 3² = 8 x 9 = 72
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, let's find the GCD of 8 and 9 using the Euclidean algorithm:
- Divide the larger number (9) by the smaller number (8): 9 ÷ 8 = 1 with a remainder of 1.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (1).
- Repeat the division: 8 ÷ 1 = 8 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 1. Therefore, GCD(8, 9) = 1.
Now, we can use the formula:
LCM(8, 9) = (8 x 9) / 1 = 72
Why is the LCM Important?
The LCM has numerous applications across various fields:
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator. This allows for a simplified calculation.
-
Cyclic Events: Imagine two events that repeat at different intervals. The LCM helps determine when both events will occur simultaneously. For instance, if one event happens every 8 days and another every 9 days, the LCM (72) indicates that both events will coincide every 72 days.
-
Music Theory: The LCM is used in music theory to determine the least common denominator for rhythmic patterns and to create harmonious combinations of notes.
-
Scheduling: In project management and scheduling, the LCM can be helpful in determining the time when various tasks with different repeating cycles will overlap.
-
Engineering: In engineering and design, LCMs are utilized in situations involving periodic phenomena, ensuring synchronization or optimal timing.
Exploring the Mathematical Concepts Behind LCM
The methods discussed above rely on fundamental number theory concepts:
-
Divisibility: A number 'a' is divisible by another number 'b' if the result of 'a' divided by 'b' is a whole number (no remainder).
-
Prime Numbers: Prime numbers are the building blocks of all other whole numbers. Understanding prime factorization is critical for efficient LCM calculation.
-
Euclidean Algorithm: This efficient algorithm is used to find the GCD of two numbers, which in turn aids in finding the LCM.
-
Fundamental Theorem of Arithmetic: This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This uniqueness is what allows the prime factorization method to work reliably.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. The GCD (Greatest Common Divisor) is the largest number that divides both numbers evenly. They are inversely related; a larger GCD means a smaller LCM and vice versa.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 4 and 8 is 8.
Q: Are there other methods to find the LCM?
A: While the methods explained are common and effective, more sophisticated algorithms exist for calculating the LCM of larger numbers or a set of more than two numbers.
Q: What if I have more than two numbers?
A: You can extend the prime factorization or GCD methods to find the LCM of more than two numbers. For the prime factorization method, consider all prime factors from all numbers, taking the highest power of each. For the GCD method, you can find the GCD of two numbers, then find the GCD of the result and the next number, and so on. Finally, use the formula relating LCM and GCD.
Q: How can I improve my understanding of LCMs?
A: Practice is key! Try calculating the LCM of various pairs of numbers using different methods. Work through example problems and try to apply the concept to real-world scenarios. Consider exploring online resources and educational materials to deepen your understanding.
Conclusion
Calculating the least common multiple (LCM) of 8 and 9, which we found to be 72, might appear simple at first glance. However, understanding the different methods – listing multiples, prime factorization, and the GCD method – provides a solid foundation for tackling more complex mathematical problems. This knowledge extends beyond simple arithmetic, proving invaluable in various fields requiring understanding of periodic events, fraction manipulation, and other mathematical applications. By mastering the concept of LCM, you'll enhance your mathematical skills and gain a deeper appreciation for the interconnectedness of mathematical concepts. Remember, consistent practice and exploration are crucial for solidifying your understanding.
Latest Posts
Latest Posts
-
Cross Section Of A Flower
Sep 21, 2025
-
3000 Acres To Square Miles
Sep 21, 2025
-
Lcm Of 2 And 7
Sep 21, 2025
-
Christmas Words Starting With E
Sep 21, 2025
-
What Times What Equals 52
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.