Lcm Of 2 And 7
seoindie
Sep 21, 2025 · 5 min read
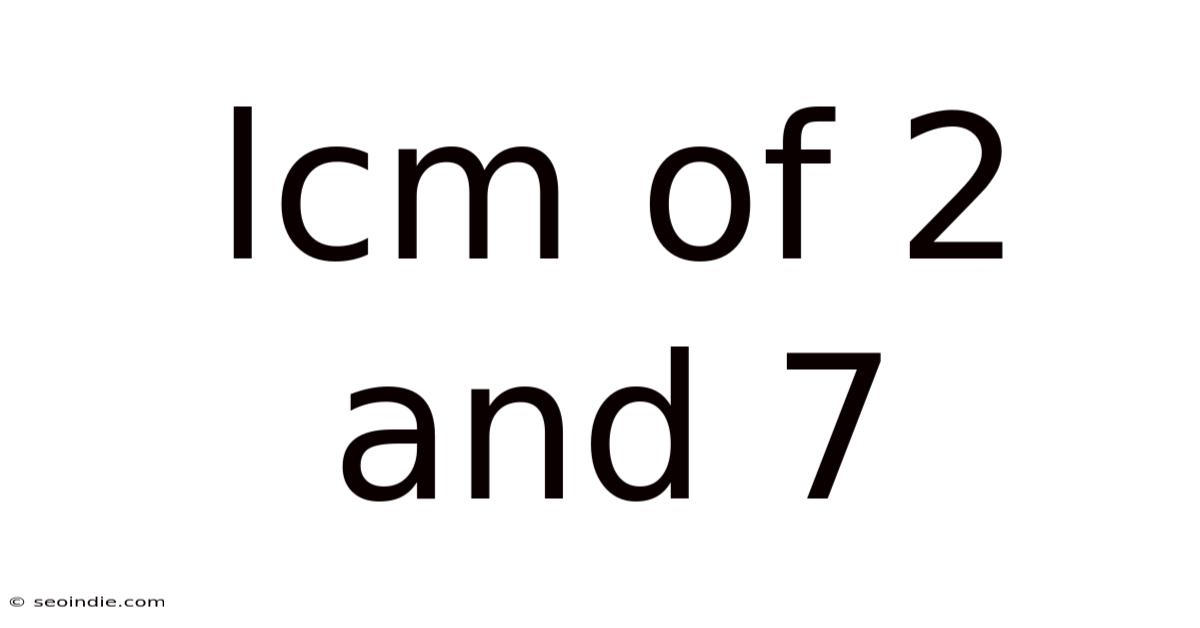
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 7: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, particularly when dealing with small numbers like 2 and 7. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for building a strong foundation in mathematics, especially when tackling more complex problems involving larger numbers or algebraic expressions. This article will delve into the LCM of 2 and 7, exploring various approaches, explaining the underlying mathematical principles, and addressing frequently asked questions. We'll also look at why understanding LCM is important beyond simple calculations.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. Think of it as finding the smallest common ground amongst different multiples.
For example, let's consider the multiples of 2 and 7:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 7: 7, 14, 21, 28, 35, 42...
Notice that 14 appears in both lists. It's the smallest number that appears in both sequences. Therefore, the LCM of 2 and 7 is 14.
Methods for Calculating the LCM of 2 and 7
Several methods can be employed to determine the LCM, each offering a different perspective on the underlying mathematical principles. Let's explore a few:
1. Listing Multiples:
This method, as demonstrated above, involves listing the multiples of each number until a common multiple is found. It's straightforward for smaller numbers but becomes cumbersome for larger numbers. This is the most intuitive method, especially for beginners.
2. Prime Factorization:
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2 (2 is a prime number itself)
- Prime factorization of 7: 7 (7 is also a prime number)
To find the LCM using prime factorization:
- Identify the prime factors: We've already done this.
- Take the highest power of each prime factor: In this case, we have 2¹ and 7¹.
- Multiply the highest powers together: 2¹ * 7¹ = 14.
Therefore, the LCM of 2 and 7 is 14. This method is more efficient for larger numbers as it avoids extensive listing.
3. Using the Formula: LCM(a, b) = (|a * b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. For 2 and 7, the GCD is 1 because 1 is the only common divisor.
- Find the GCD of 2 and 7: GCD(2, 7) = 1
- Apply the formula: LCM(2, 7) = (|2 * 7|) / 1 = 14
This formula provides a direct and efficient way to calculate the LCM, especially when dealing with larger numbers where finding the GCD might be easier than listing multiples or finding prime factorizations.
The Significance of LCM in Everyday Life and Advanced Mathematics
While the LCM of 2 and 7 might seem trivial, the concept of LCM is fundamental to various aspects of mathematics and beyond:
-
Scheduling and Timing: Imagine two buses arriving at a bus stop; one every 2 hours and the other every 7 hours. The LCM helps determine when both buses will arrive simultaneously, making it crucial for scheduling and planning.
-
Fractions and Ratios: Finding the LCM is essential when adding or subtracting fractions with different denominators. We find the LCM of the denominators to create a common denominator, simplifying the calculations.
-
Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Algebra and Abstract Algebra: The concept of LCM extends to more complex mathematical structures, including rings and ideals, in abstract algebra.
Frequently Asked Questions (FAQ)
Q1: Is there only one LCM for two numbers?
A1: Yes, there's only one least common multiple for any given set of numbers. While there are many common multiples, only one is the smallest.
Q2: What is the LCM of a number and itself?
A2: The LCM of a number and itself is the number itself. For example, LCM(5, 5) = 5.
Q3: What if one of the numbers is zero?
A3: The LCM is undefined when one of the numbers is zero. The concept of multiples doesn't apply to zero in the same way.
Q4: How can I find the LCM of more than two numbers?
A4: For more than two numbers, you can extend the prime factorization method or use iterative application of the LCM formula. For instance, to find the LCM of 2, 7, and 3, you would first find the LCM of 2 and 7 (which is 14), and then find the LCM of 14 and 3. The prime factorization method is generally easier to extend for multiple numbers.
Conclusion
Determining the least common multiple of 2 and 7, while seemingly simple, provides a valuable gateway to understanding more complex mathematical concepts. The various methods discussed—listing multiples, prime factorization, and using the GCD formula—offer different approaches to solving the problem, highlighting the diverse tools available in mathematics. The application of LCM extends far beyond basic arithmetic, playing a critical role in various fields, showcasing its practical significance in daily life and advanced mathematical applications. Mastering the concept of LCM is a significant step towards building a robust mathematical foundation and developing problem-solving skills applicable in a variety of contexts. Remember to practice these methods with different numbers to solidify your understanding and build confidence in tackling more challenging LCM problems.
Latest Posts
Latest Posts
-
Words That Start With Start
Sep 21, 2025
-
5 Letter Word Starting O
Sep 21, 2025
-
Lewis Structure For Nitric Acid
Sep 21, 2025
-
Nouns That End With Ing
Sep 21, 2025
-
One Hundred And Thirty Dollars
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.