Lcm For 7 And 11
seoindie
Sep 16, 2025 · 5 min read
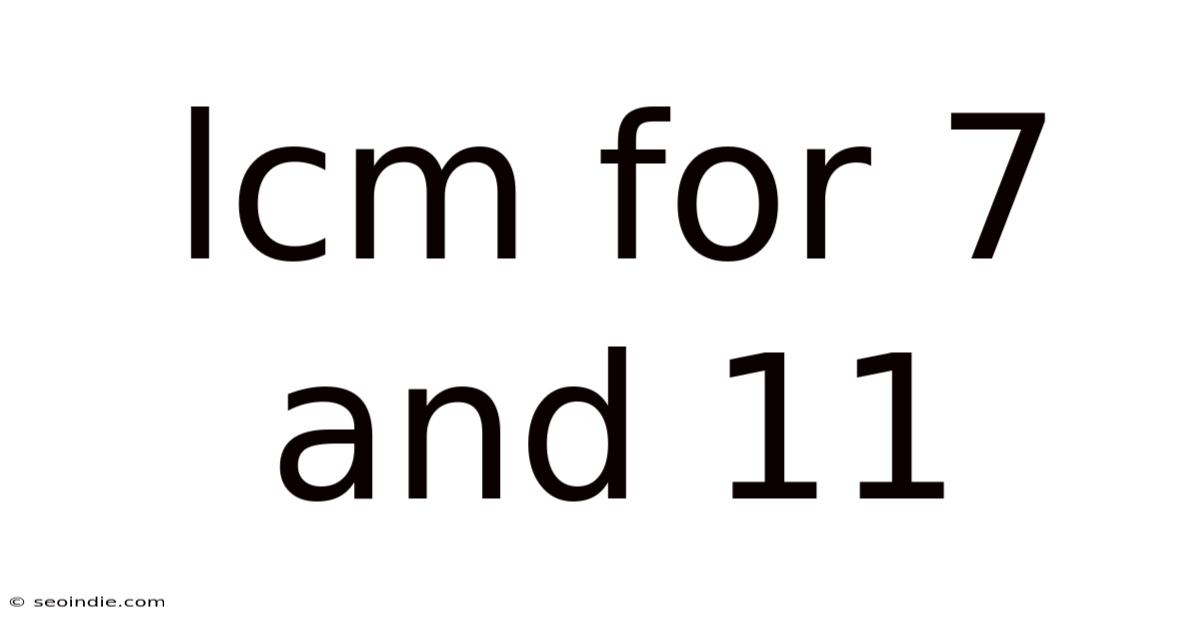
Table of Contents
Unveiling the Least Common Multiple (LCM) of 7 and 11: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles provides a powerful foundation for more advanced mathematical concepts. This article will explore the LCM of 7 and 11, not just by providing the answer, but by delving into the methods, the theory behind them, and the broader applications of LCM in various fields. We'll also address frequently asked questions and demonstrate the elegance and practicality of this fundamental mathematical operation.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is crucial in various mathematical operations and real-world applications, from scheduling events to solving complex algebraic equations.
Methods for Finding the LCM of 7 and 11
There are several approaches to determine the LCM of 7 and 11. Let's explore the most common methods:
1. Listing Multiples Method:
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88...
By comparing the lists, we observe that the smallest number present in both lists is 77. Therefore, the LCM of 7 and 11 is 77.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 11: 11 (11 is a prime number)
Since 7 and 11 are both prime numbers, their prime factorizations are simply themselves. To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case:
LCM(7, 11) = 7 * 11 = 77
3. Greatest Common Divisor (GCD) Method:
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD). The GCD is the largest number that divides both integers without leaving a remainder. For 7 and 11, the GCD is 1 because they share no common divisors other than 1. The relationship between LCM and GCD is expressed by the formula:
LCM(a, b) * GCD(a, b) = a * b
Substituting the values for 7 and 11:
LCM(7, 11) * GCD(7, 11) = 7 * 11 LCM(7, 11) * 1 = 77 LCM(7, 11) = 77
Why is the LCM of 7 and 11 equal to 77? A Deeper Look
The LCM of 7 and 11 being 77 is a direct consequence of the fact that 7 and 11 are relatively prime or coprime. Two numbers are relatively prime if their greatest common divisor (GCD) is 1. Because 7 and 11 are both prime numbers and have no common factors other than 1, their LCM is simply their product. This is a crucial property to remember when dealing with prime numbers and their multiples.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine you have two events: one occurs every 7 days and another every 11 days. To find when both events coincide, you need to determine the LCM(7, 11) = 77. Both events will occur on the same day again after 77 days.
-
Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Music Theory: The LCM is used in music theory to determine the least common multiple of note durations, useful in calculating rhythmic patterns and harmonies.
-
Engineering and Construction: LCM helps in coordinating tasks with different cycle times in projects, ensuring efficient resource allocation.
-
Computer Science: LCM plays a role in algorithms related to scheduling processes and managing system resources.
Frequently Asked Questions (FAQs)
Q: Is the LCM always greater than the two numbers?
A: Yes, the LCM is always greater than or equal to the larger of the two numbers. If the two numbers are the same, then the LCM is equal to the number.
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the methods discussed above to find the LCM of more than two numbers. The prime factorization method is particularly efficient for multiple numbers. You find the prime factorization of each number and then take the highest power of each prime factor present across all factorizations and multiply them together.
Q: What's the difference between LCM and GCD?
A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related through the formula: LCM(a, b) * GCD(a, b) = a * b
Q: Can the LCM of two numbers be negative?
A: No, the LCM is always a positive integer.
Q: Are there any shortcuts for finding the LCM of larger numbers?
A: While the prime factorization method is generally efficient, there are more advanced algorithms like the Euclidean algorithm (often used to find the GCD first, and then calculate the LCM using the relationship mentioned above) that are optimized for larger numbers and offer improved computational speed. These algorithms are usually implemented in computer programs.
Conclusion:
The LCM of 7 and 11, calculated to be 77, serves as a simple yet illustrative example of a fundamental mathematical concept. Understanding the different methods for calculating the LCM, particularly the prime factorization method, allows for a deeper comprehension of the underlying principles and facilitates the application of LCM to various real-world problems across various disciplines. The concept of relative primality and its relationship to the LCM enhances the understanding of numerical relationships and provides a solid groundwork for more advanced mathematical explorations. This seemingly basic concept, therefore, forms a crucial building block in mathematics and its numerous practical applications.
Latest Posts
Latest Posts
-
The Prime Factorization Of 42
Sep 16, 2025
-
What Times What Equals 22
Sep 16, 2025
-
How Is Polygenic Inheritance Defined
Sep 16, 2025
-
What Is Threading In Os
Sep 16, 2025
-
Lcm 8 10 And 12
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 7 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.