Lcm 8 10 And 12
seoindie
Sep 16, 2025 · 6 min read
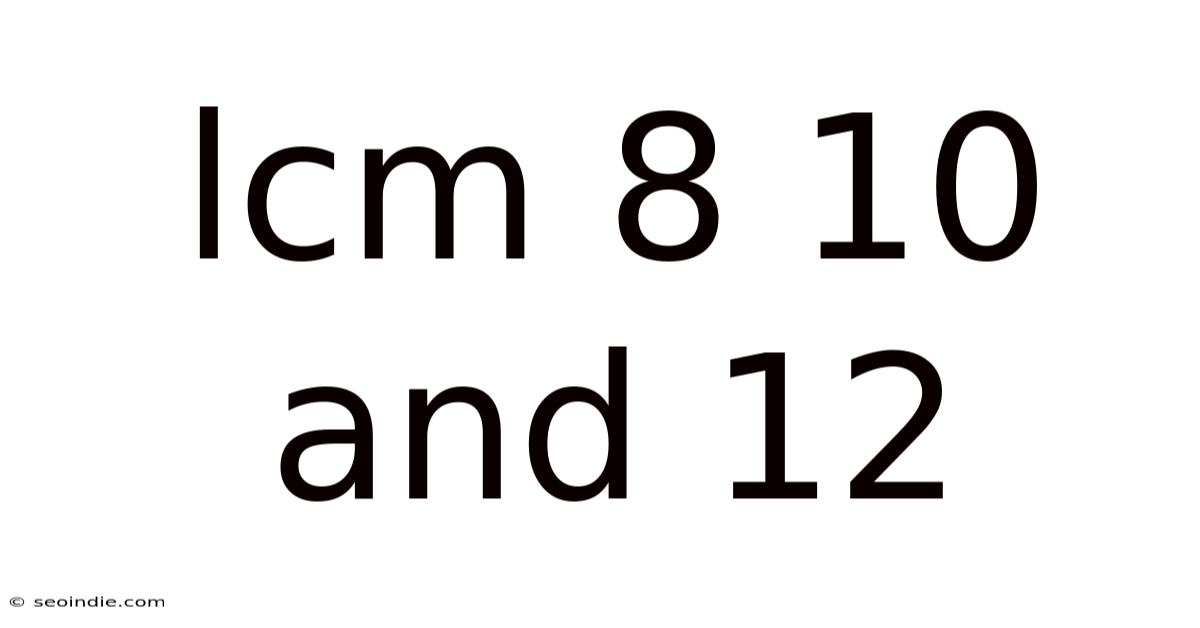
Table of Contents
Finding the LCM of 8, 10, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex scheduling problems. This article provides a comprehensive guide to finding the LCM of 8, 10, and 12, exploring different methods and delving into the underlying mathematical principles. We'll not only show you how to find the LCM but also why these methods work, ensuring a thorough understanding of this important topic. Understanding LCM is essential for anyone studying arithmetic, algebra, or even venturing into more advanced mathematical fields.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 8, 10, and 12, let's clarify the concept. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. This concept is vital in various real-world scenarios, such as determining the least amount of time it takes for events to occur simultaneously or finding the smallest quantity needed to fulfill multiple requirements.
Method 1: Listing Multiples
This method is the most straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
By comparing the lists, we see that the smallest number appearing in all three lists is 120. Therefore, the LCM of 8, 10, and 12 is 120.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It relies on expressing each number as a product of its prime factors. Prime factorization breaks a number down into its smallest prime number building blocks.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
- 12 = 2 x 2 x 3 = 2² x 3
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 8, 10, and 12, using prime factorization, is 120. This method is particularly useful because it highlights the fundamental building blocks of the numbers and reveals why the LCM is what it is. It's not just a coincidence; it's a direct result of the prime factorization.
Method 3: Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD). The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a formula that elegantly connects the LCM and GCD:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c) (This formula is for three numbers. For two numbers, you would simply use LCM(a,b) = (a x b)/GCD(a,b))
-
Find the GCD of 8, 10, and 12:
We can use the Euclidean algorithm to find the GCD. This involves repeatedly applying the division algorithm until the remainder is 0. However, for smaller numbers, we can often find the GCD by inspection. The largest number that divides 8, 10, and 12 is 2. Therefore, GCD(8, 10, 12) = 2.
-
Apply the formula:
LCM(8, 10, 12) = (8 x 10 x 12) / GCD(8, 10, 12) = (960) / 2 = 120
Again, the LCM of 8, 10, and 12 is 120. This method demonstrates a powerful relationship between LCM and GCD, highlighting the interconnectedness of these core mathematical concepts. It showcases how efficient mathematical tools can significantly simplify calculations.
Applications of LCM
The concept of LCM has wide-ranging applications across various fields:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Scheduling Problems: Determining when events will coincide, such as the simultaneous departure of buses from different terminals, often requires finding the LCM.
- Cyclic Patterns: Analyzing repeating patterns or cycles, such as the periodic repetition of events, uses the LCM to identify when the patterns will align.
- Gear Ratios: In mechanics, determining gear ratios and the synchronization of rotating parts involves calculating LCMs.
- Music Theory: Understanding musical intervals and harmonies involves concepts related to LCM.
- Computer Science: Algorithms related to synchronization and scheduling often utilize the LCM concept.
Why Understanding LCM is Important
Beyond the immediate applications, mastering the LCM concept fosters crucial problem-solving skills. It encourages analytical thinking, the ability to break down complex problems into smaller, manageable parts, and the development of strategic approaches to problem-solving. This is not just about memorizing formulas; it's about understanding the underlying mathematical principles and their practical relevance.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple of a set of numbers, while the GCD is the greatest common divisor. They are inversely related, and understanding one helps understand the other.
-
Can I use a calculator to find the LCM? Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of numbers. However, understanding the methods described above is crucial for comprehending the underlying mathematics.
-
What if I have more than three numbers? The prime factorization method and the GCD method can be easily extended to handle more than three numbers. The multiple listing method becomes less practical with a larger number of inputs.
-
Why is prime factorization so important in finding the LCM? Because prime numbers are the fundamental building blocks of all integers. By breaking down numbers into their prime factors, we can systematically identify the smallest combination of those factors that contains all the factors of the original numbers.
-
Is there only one LCM for a set of numbers? Yes, there is only one least common multiple for any given set of integers.
Conclusion
Finding the LCM of 8, 10, and 12, as demonstrated above, is more than just a simple arithmetic exercise. It’s an opportunity to explore fundamental mathematical principles, develop problem-solving skills, and appreciate the practical applications of these concepts across various disciplines. Whether you use the method of listing multiples, prime factorization, or the GCD method, the result remains the same: the LCM of 8, 10, and 12 is 120. However, understanding why this is true, and how the different methods connect, is essential for a comprehensive understanding of this vital mathematical concept. The journey to mastering LCM isn't just about getting the right answer; it's about gaining a deeper appreciation for the elegant structure and interconnectedness of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm 8 10 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.