Hcf Of 60 And 72
seoindie
Sep 12, 2025 · 6 min read
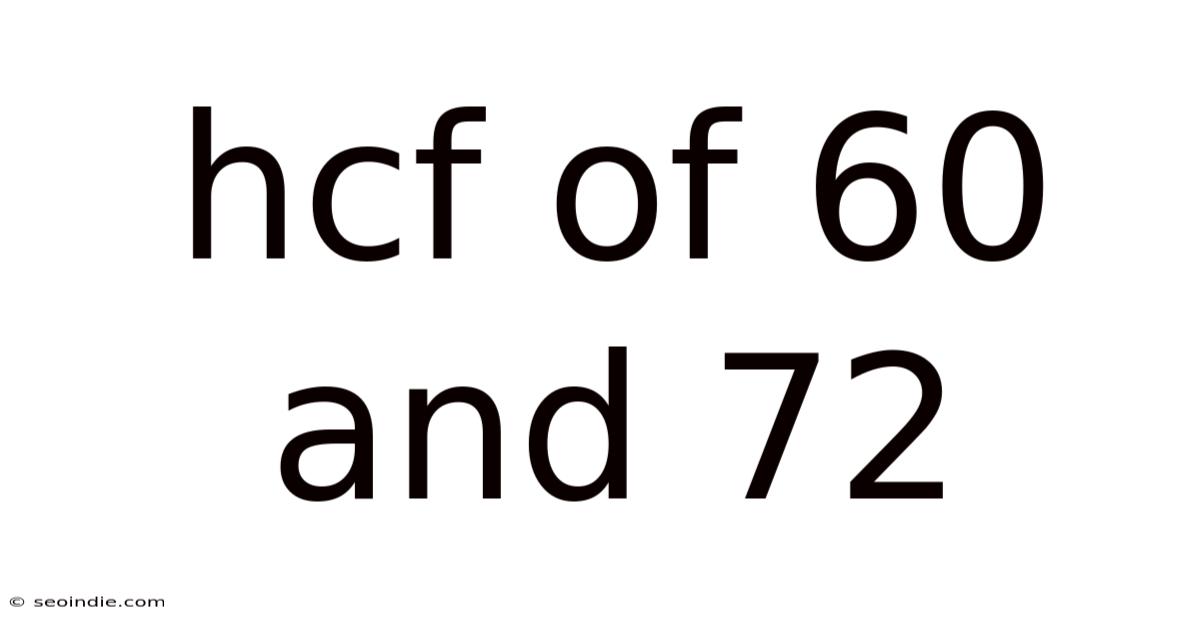
Table of Contents
Finding the Highest Common Factor (HCF) of 60 and 72: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving complex algebraic problems. This article will provide a thorough understanding of how to calculate the HCF of 60 and 72, exploring multiple methods and delving into the underlying mathematical principles. We'll cover prime factorization, the Euclidean algorithm, and explore the practical significance of understanding HCFs.
Understanding Highest Common Factor (HCF)
Before we dive into calculating the HCF of 60 and 72, let's define what it means. The HCF of two or more numbers is the largest number that divides each of them without leaving a remainder. Think of it as the biggest common divisor these numbers share. For example, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The highest among these is 6, so the HCF of 12 and 18 is 6.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. The HCF is then found by identifying the common prime factors and multiplying them together.
Let's apply this to 60 and 72:
1. Prime Factorization of 60:
- We start by dividing 60 by the smallest prime number, 2: 60 ÷ 2 = 30
- We continue dividing by 2: 30 ÷ 2 = 15
- Now, 15 is not divisible by 2, so we move to the next prime number, 3: 15 ÷ 3 = 5
- 5 is a prime number, so the prime factorization of 60 is 2 x 2 x 3 x 5, or 2² x 3 x 5.
2. Prime Factorization of 72:
- We start with 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 is not divisible by 2, so we use 3: 9 ÷ 3 = 3
- 3 is a prime number, so the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, or 2³ x 3².
3. Finding the Common Factors:
Comparing the prime factorizations of 60 (2² x 3 x 5) and 72 (2³ x 3²), we see that they share two 2s and one 3.
4. Calculating the HCF:
Multiplying the common prime factors together: 2 x 2 x 3 = 12.
Therefore, the HCF of 60 and 72 is 12.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF, especially for larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply this to 60 and 72:
1. Repeated Subtraction:
- Start with the larger number (72) and repeatedly subtract the smaller number (60) until the result is less than 60: 72 - 60 = 12
- Now, we have the numbers 60 and 12. Repeat the process: 60 - 12 = 48
- 48 - 12 = 36
- 36 - 12 = 24
- 24 - 12 = 12
- Now we have 12 and 12. Since both numbers are the same, the HCF is 12.
2. More Efficient Euclidean Algorithm (Division Method):
The repeated subtraction can be cumbersome for larger numbers. A more efficient approach uses division with remainders:
- Divide the larger number (72) by the smaller number (60): 72 ÷ 60 = 1 with a remainder of 12.
- Now, replace the larger number with the smaller number (60) and the smaller number with the remainder (12): 60 ÷ 12 = 5 with a remainder of 0.
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 12.
Method 3: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. While effective for smaller numbers, it becomes less practical for larger ones.
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
By comparing the lists, we see that the largest common factor is 12.
The Significance of HCF
Understanding and calculating the HCF has various practical applications:
-
Simplifying Fractions: The HCF helps in reducing fractions to their simplest form. For example, the fraction 60/72 can be simplified by dividing both the numerator and the denominator by their HCF (12), resulting in the equivalent fraction 5/6.
-
Solving Word Problems: Many real-world problems involve finding the largest common divisor. For instance, imagine you have 60 red marbles and 72 blue marbles, and you want to divide them into identical bags with the maximum number of marbles in each bag of the same color. The HCF (12) indicates you can create 12 bags, each containing 5 red and 6 blue marbles.
-
Geometry and Measurement: HCF is used in determining the dimensions of objects or finding the greatest possible length for tiles when covering a rectangular area.
-
Number Theory: HCF is a fundamental concept in number theory, used in solving various mathematical problems related to divisibility and prime numbers.
Frequently Asked Questions (FAQ)
Q1: What if the HCF of two numbers is 1?
A1: If the HCF of two numbers is 1, it means they are relatively prime or coprime. This indicates that they share no common factors other than 1.
Q2: Can the HCF of two numbers be greater than the smaller number?
A2: No. The HCF can never be greater than the smaller of the two numbers. The HCF is, by definition, a divisor of both numbers.
Q3: Is there a formula to calculate the HCF?
A3: There isn't a single, universally applicable formula for calculating the HCF. The methods described above (prime factorization, Euclidean algorithm, listing factors) are the most common approaches. However, more advanced algorithms exist for very large numbers.
Q4: How do I find the HCF of more than two numbers?
A4: To find the HCF of more than two numbers, you can extend the Euclidean algorithm or use prime factorization. Find the HCF of the first two numbers, then find the HCF of that result and the third number, and so on.
Conclusion
Finding the HCF of 60 and 72, as demonstrated using various methods, highlights the importance of understanding this fundamental mathematical concept. Whether you use prime factorization, the Euclidean algorithm, or the listing factor method, the HCF will always be 12. This knowledge extends beyond simple calculations; it underpins our understanding of fractions, problem-solving, and many areas of advanced mathematics. The ability to efficiently calculate the HCF is a valuable skill for anyone seeking a deeper understanding of numbers and their relationships. Mastering these techniques equips you to tackle more complex mathematical problems with confidence and precision.
Latest Posts
Latest Posts
-
Meaning Of Mutually Exclusive Events
Sep 13, 2025
-
Chemical Reactions In Everyday Life
Sep 13, 2025
-
How Much Is 12 Centimeters
Sep 13, 2025
-
Complete Dominance And Incomplete Dominance
Sep 13, 2025
-
Lcm Of 3 5 6
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 60 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.