Lcm Of 3 5 6
seoindie
Sep 13, 2025 · 6 min read
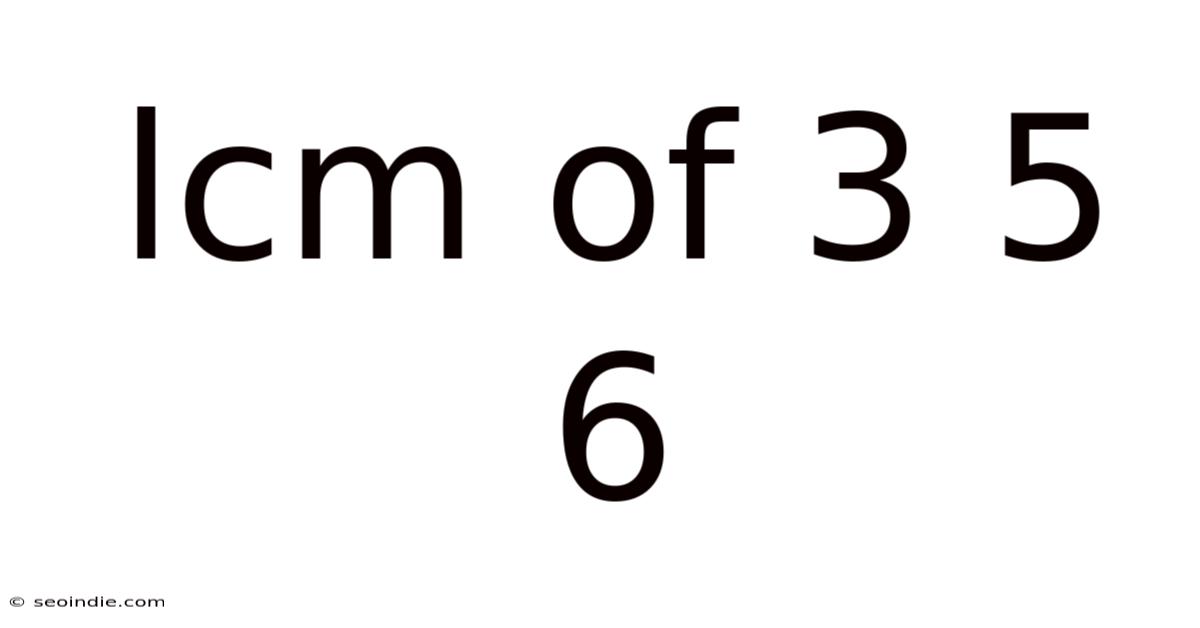
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications across various fields, from scheduling tasks to understanding rhythmic patterns in music. This comprehensive guide will delve into the process of calculating the LCM of 3, 5, and 6, explaining different methods and providing a deeper understanding of the underlying principles. We'll cover everything from basic definitions to advanced techniques, ensuring a thorough understanding for learners of all levels.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems related to cycles and repetitions, and even in more advanced areas like abstract algebra.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers. Let's find the LCM of 3, 5, and 6 using this approach:
-
List the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, ...
-
Identify common multiples: Look for the numbers that appear in all three lists. We see that 30 is the smallest number present in all three lists.
-
Conclusion: Therefore, the LCM of 3, 5, and 6 is 30.
This method is effective for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a more systematic approach. It relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Find the prime factorization of each number:
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 6 = 2 x 3
-
Identify the highest power of each prime factor: We have the prime factors 2, 3, and 5. The highest power of 2 is 2<sup>1</sup>, the highest power of 3 is 3<sup>1</sup>, and the highest power of 5 is 5<sup>1</sup>.
-
Multiply the highest powers together: LCM(3, 5, 6) = 2<sup>1</sup> x 3<sup>1</sup> x 5<sup>1</sup> = 2 x 3 x 5 = 30
Therefore, the LCM of 3, 5, and 6 is 30. This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, but it becomes more complex. Let's illustrate how to use this for our example, but focusing on pairs of numbers to simplify:
-
Find the GCD of pairs of numbers:
- GCD(3, 5) = 1 (3 and 5 have no common factors other than 1)
- GCD(3, 6) = 3
- GCD(5, 6) = 1
-
Apply the LCM-GCD relationship: While the direct application of the formula to three numbers is more involved, we can use it iteratively. Let's find the LCM of 3 and 5 first.
- LCM(3,5) x GCD(3,5) = 3 x 5
- LCM(3,5) x 1 = 15
- LCM(3,5) = 15
-
Now, find the LCM of 15 and 6:
- LCM(15,6) x GCD(15,6) = 15 x 6
- LCM(15,6) x 3 = 90
- LCM(15,6) = 30
Therefore, the LCM of 3, 5, and 6 is 30. This method shows the interconnectedness of LCM and GCD, but the prime factorization method is generally more straightforward for multiple numbers.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method is powerful because it leverages the fundamental building blocks of numbers – prime numbers. Prime numbers are integers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). The fundamental theorem of arithmetic guarantees that every composite number (a number that is not prime) can be uniquely expressed as a product of prime numbers.
This unique factorization allows us to systematically find the LCM. By identifying the highest power of each prime factor present in the numbers, we ensure that the resulting LCM contains all the necessary factors to be divisible by each of the original numbers. This method works flawlessly regardless of the size of the numbers involved.
Applications of LCM in Real-World Scenarios
The concept of LCM has practical applications in various fields:
-
Scheduling: Imagine you have three machines that perform different tasks in a manufacturing process. Machine A completes a cycle every 3 hours, Machine B every 5 hours, and Machine C every 6 hours. To find when all three machines will complete a cycle simultaneously, you need to find the LCM(3, 5, 6) = 30. All three machines will complete a cycle together after 30 hours.
-
Rhythmic patterns: In music, LCM is used to find the least common denominator for rhythmic patterns. If you have three musical phrases with lengths of 3, 5, and 6 beats respectively, the LCM will determine the shortest length at which all three phrases will repeat simultaneously.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps in finding a common denominator for simplifying the calculation.
-
Modular Arithmetic: LCM plays a critical role in solving congruences and other problems in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have a common factor greater than 1? A: The LCM will be smaller than simply multiplying the numbers together. The prime factorization method efficiently handles this scenario by only including the highest power of each prime factor.
-
Q: Can I use this method for more than three numbers? A: Absolutely! The prime factorization method extends seamlessly to any number of integers. Simply find the prime factorization of each number, identify the highest power of each prime factor, and multiply them together.
-
Q: What is the difference between LCM and GCD? A: The LCM is the smallest number that is a multiple of all given numbers, while the GCD is the largest number that is a divisor of all given numbers. They are inversely related; a larger GCD implies a smaller LCM and vice-versa.
-
Q: Are there any online calculators for LCM? A: Yes, many websites and online calculators can compute the LCM of numbers. However, understanding the underlying method is essential for applying the concept in various contexts and solving more complex problems.
Conclusion
Finding the LCM of 3, 5, and 6, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. The prime factorization method stands out as the most efficient and versatile technique for determining the LCM of any set of integers. Mastering this concept opens doors to understanding more advanced mathematical ideas and solving real-world problems across diverse fields. While calculators can provide quick solutions, a deep grasp of the underlying principles empowers you to tackle more complex problems with confidence and insight. Remember, the beauty of mathematics lies not just in the answers, but in the journey of understanding the 'why' behind the solutions.
Latest Posts
Latest Posts
-
Highest Mountain Range On Earth
Sep 13, 2025
-
How Many Inches Is 148cm
Sep 13, 2025
-
What Times What Makes 72
Sep 13, 2025
-
Difference Between Actin And Myosin
Sep 13, 2025
-
How Much Is 100 000
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.