Gcf Of 18 And 54
seoindie
Sep 23, 2025 · 6 min read
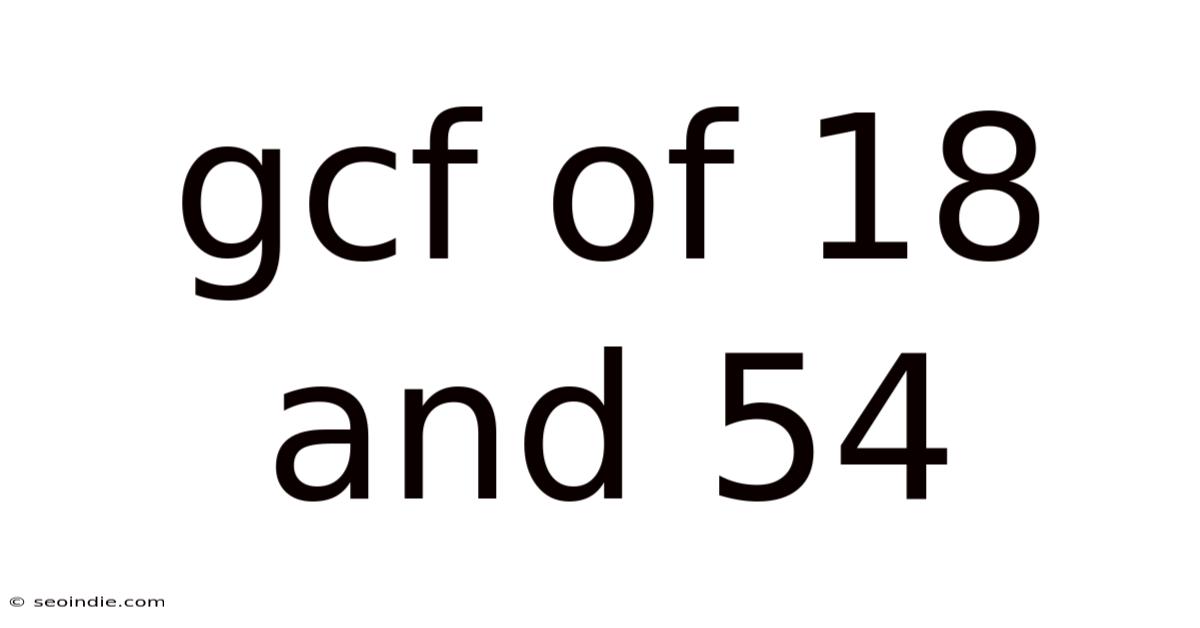
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 18 and 54: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and different methods for calculating the GCF provides a valuable foundation in number theory and is crucial for various mathematical applications. This comprehensive guide delves into finding the GCF of 18 and 54, exploring multiple approaches and providing a deeper understanding of the concept. We will cover various methods, including listing factors, prime factorization, and the Euclidean algorithm, ensuring you grasp the core concepts and can apply them to other number pairs.
Understanding Greatest Common Factors (GCF)
Before we dive into calculating the GCF of 18 and 54, let's establish a solid understanding of what a GCF actually represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest among these is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Comparing the two lists, we find the common factors are 1, 2, 3, 6, 9, and 18. The largest among these is 18.
Therefore, the GCF of 18 and 54 is 18.
Method 2: Prime Factorization
This method uses the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 18 and 54:
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³
To find the GCF using prime factorization, we identify the common prime factors and take the lowest power of each. Both 18 and 54 share a factor of 2 and a factor of 3².
Therefore, the GCF is 2¹ x 3² = 2 x 9 = 18.
Again, we confirm that the GCF of 18 and 54 is 18.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 18 and 54:
- Start with the larger number (54) and the smaller number (18).
- Divide the larger number by the smaller number and find the remainder: 54 ÷ 18 = 3 with a remainder of 0.
Since the remainder is 0, the smaller number (18) is the GCF.
Therefore, the GCF of 18 and 54 is 18.
Visualizing the GCF: Using Area Models
A visual approach can enhance understanding, particularly for those who benefit from graphical representations. Imagine you have a rectangular area. One side measures 18 units and the other 54 units. The area of the rectangle represents the product of the two numbers (18 x 54 = 972). The GCF represents the side length of the largest square that can perfectly tile this rectangle without any gaps or overlaps. In this case, you could tile the rectangle with 18 x 18 squares, indicating that 18 is the GCF. Each side of the larger rectangle would be divisible by 18, hence proving the GCF.
Applications of GCF in Real-World Scenarios
The concept of GCF isn't confined to abstract mathematical exercises. It has practical applications in various real-world situations:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For instance, the fraction 54/18 can be simplified by dividing both the numerator and denominator by their GCF (18), resulting in the simplified fraction 3/1 or simply 3.
-
Dividing Objects Equally: Imagine you have 54 apples and 18 oranges, and you want to divide them into equally sized bags without any leftovers. The GCF (18) tells you that you can create 18 bags, each containing 3 apples and 1 orange.
-
Measurement and Construction: In construction or design, determining the GCF can help in finding the largest common unit for measuring or cutting materials efficiently, minimizing waste and ensuring precision.
Extending the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and identify the common prime factors with their lowest powers. For the Euclidean algorithm, you would repeatedly apply the process to pairs of numbers until you find the GCF.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q2: Are there any limitations to the Euclidean algorithm?
A2: While highly efficient, the Euclidean algorithm is primarily suited for integer calculations. It’s not directly applicable to finding the GCF of irrational or complex numbers.
Q3: Can I use a calculator to find the GCF?
A3: Yes, many calculators, especially scientific calculators, have built-in functions to calculate the GCF of two or more numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill in mathematics. Understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – provides flexibility and efficiency in tackling various problems. Beyond the theoretical understanding, appreciating the practical applications of GCF in everyday situations underscores its importance and relevance in various fields. By mastering these techniques, you’ll not only enhance your mathematical proficiency but also develop a deeper appreciation for the elegance and power of number theory. The GCF of 18 and 54, as we've demonstrated through multiple methods, is undeniably 18, a result that reinforces the core principles of this important mathematical concept. Continue to practice these methods with different number pairs, and you'll soon find yourself confidently calculating GCFs with ease and understanding.
Latest Posts
Latest Posts
-
Dehydration Of 1 Methyl Cyclohexanol
Sep 23, 2025
-
Adverbs That Start With R
Sep 23, 2025
-
Capacitance Of A Cylindrical Capacitor
Sep 23, 2025
-
The Smooth Er Possesses Ribosomes
Sep 23, 2025
-
How To Find Oblique Asymptotes
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 18 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.