Gcf Of 12 And 3
seoindie
Sep 25, 2025 · 6 min read
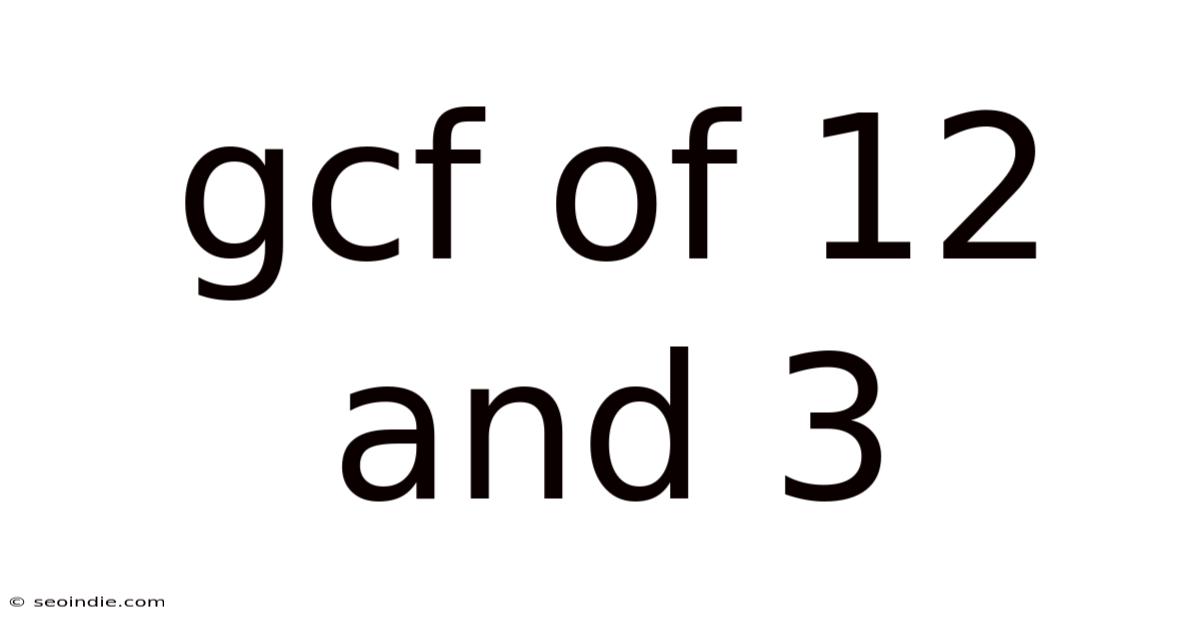
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 12 and 3: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task, especially when dealing with small numbers like 12 and 3. However, understanding the underlying concepts and different methods for finding the GCF provides a foundational understanding of number theory, crucial for advanced mathematical concepts. This article will not only determine the GCF of 12 and 3 but also explore various approaches, explain the underlying mathematical principles, and address frequently asked questions. This in-depth exploration will equip you with a solid grasp of GCF calculations and their significance.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding this fundamental concept is key to tackling more complex problems in algebra, number theory, and other mathematical fields.
Methods for Finding the GCF of 12 and 3
Several methods can effectively determine the GCF. Let's explore the most common ones, applying them to find the GCF of 12 and 3:
1. Listing Factors:
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 3: 1, 3
Comparing the lists, we see that the common factors are 1 and 3. The largest common factor is 3. Therefore, the GCF of 12 and 3 is 3.
2. Prime Factorization:
This method involves finding the prime factorization of each number and then multiplying the common prime factors raised to the lowest power.
- Prime factorization of 12: 2² x 3
- Prime factorization of 3: 3
The only common prime factor is 3. Both numbers have at least one 3. Therefore, the GCF is 3. This method is particularly useful for larger numbers where listing factors becomes cumbersome.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 3:
- 12 ÷ 3 = 4 with a remainder of 0. Since the remainder is 0, the GCF is the smaller number, which is 3.
This algorithm is remarkably efficient because it avoids the need for complete factorization and directly leads to the GCF.
The GCF of 12 and 3: A Detailed Explanation
As demonstrated by all three methods, the GCF of 12 and 3 is unequivocally 3. This is because 3 is the largest integer that divides both 12 and 3 without leaving a remainder. 12 can be expressed as 3 x 4, and 3 can be expressed as 3 x 1. No larger integer can achieve this division without a remainder.
Illustrative Examples and Applications
Understanding the GCF has practical applications in various areas:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For instance, the fraction 12/3 can be simplified to 4/1 (or simply 4) by dividing both the numerator and denominator by their GCF, which is 3.
-
Problem Solving: Many word problems in mathematics involve finding the GCF to solve real-world scenarios. For example, you might need to find the largest square tiles that can perfectly cover a rectangular floor of dimensions 12 feet by 3 feet. The GCF of 12 and 3 (which is 3) would give you the side length of the largest square tile.
-
Geometric Applications: GCF is crucial in geometry when dealing with problems involving area and volume calculations, finding common measures, or determining the dimensions of shapes.
-
Abstract Algebra: The concept of GCF extends to abstract algebra, where it forms a foundation for understanding ideals and rings.
Beyond the Basics: Exploring Further Concepts
While finding the GCF of 12 and 3 is straightforward, the concept extends to more complex scenarios:
-
Finding the GCF of More Than Two Numbers: The methods described above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 12, 3, and 6, you would find the GCF of 12 and 3 (which is 3), and then find the GCF of 3 and 6 (which is 3). Therefore, the GCF of 12, 3, and 6 is 3.
-
Using the GCF in Least Common Multiple (LCM) Calculations: The GCF and LCM (Least Common Multiple) are closely related. The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. This relationship is valuable for solving problems involving both GCF and LCM. The formula is: GCF(a, b) * LCM(a, b) = a * b
-
Applications in Cryptography: The concept of GCF plays a significant role in cryptography, especially in algorithms that rely on the properties of prime numbers and modular arithmetic.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they share no common factors other than 1. For example, 12 and 7 are relatively prime because their GCF is 1.
Q2: Can the GCF of two numbers be larger than either number?
A2: No. The GCF of two numbers is always less than or equal to the smaller of the two numbers.
Q3: Are there any limitations to the Euclidean Algorithm?
A3: While highly efficient for most numbers, the Euclidean Algorithm can become computationally intensive for extremely large numbers, particularly in contexts where computational resources are limited.
Conclusion
Determining the greatest common factor of 12 and 3, while seemingly a simple exercise, provides a valuable entry point into the fascinating world of number theory. This article has not only demonstrated how to find the GCF using various methods but also explored the underlying principles, applications, and related concepts. Understanding the GCF is essential for simplifying fractions, solving various mathematical problems, and laying the foundation for more advanced mathematical studies. By mastering these concepts, you equip yourself with a powerful tool for navigating and understanding the intricacies of numbers. Remember, the journey into mathematics is a continuous process of exploration and discovery, and the seemingly simple GCF holds a key to unlocking a world of deeper mathematical understanding.
Latest Posts
Latest Posts
-
3 Times What Equals 72
Sep 25, 2025
-
Parallel Vs Antiparallel Beta Sheets
Sep 25, 2025
-
What Does 5cm Look Like
Sep 25, 2025
-
Gene Knockdown Vs Gene Knockout
Sep 25, 2025
-
2 Times What Equals 36
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.