First Four Multiples Of 6
seoindie
Sep 23, 2025 · 7 min read
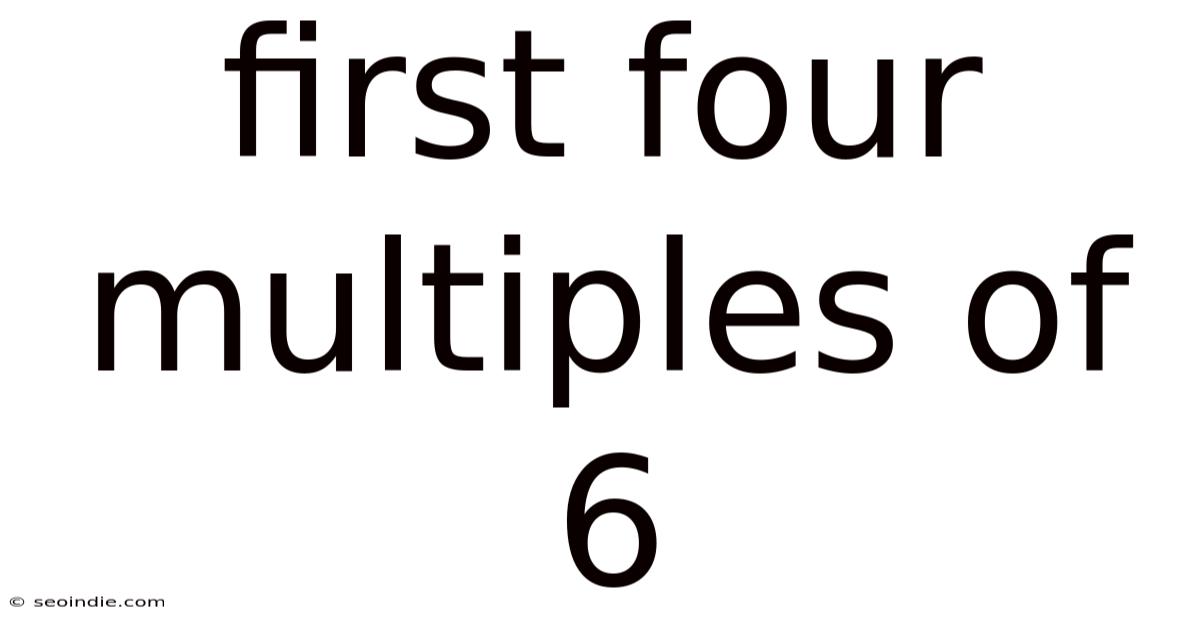
Table of Contents
Unveiling the Secrets of the First Four Multiples of 6: A Deep Dive into Multiplication
Understanding multiplication is a cornerstone of mathematical literacy, opening doors to a vast world of numerical relationships and problem-solving. This article delves into the seemingly simple concept of the first four multiples of 6, exploring not just the calculations but also the underlying principles, practical applications, and the broader mathematical context. We’ll examine why understanding multiples is crucial, explore various methods for calculating them, and even delve into some fascinating real-world examples. By the end, you’ll not only know the first four multiples of 6 but also possess a much deeper understanding of multiplication itself.
What are Multiples? A Foundational Concept
Before we jump into the specifics of the first four multiples of 6, let’s establish a clear understanding of what a multiple is. Simply put, a multiple of a number is the result of multiplying that number by any whole number (0, 1, 2, 3, and so on). So, multiples represent the products obtained when a specific number is repeatedly added to itself. For example, the multiples of 2 are 0, 2, 4, 6, 8, 10, and so on. Each of these numbers is obtained by multiplying 2 by a whole number (2 x 0 = 0, 2 x 1 = 2, 2 x 2 = 4, and so on).
The concept of multiples is fundamental to various mathematical operations and applications. It underpins our understanding of factors, divisibility rules, and even more advanced concepts like least common multiples (LCM) and greatest common divisors (GCD).
Calculating the First Four Multiples of 6: A Step-by-Step Guide
Now, let’s get to the heart of the matter: the first four multiples of 6. This involves multiplying 6 by the first four whole numbers: 0, 1, 2, and 3.
- First Multiple (6 x 0): 6 multiplied by 0 equals 0. This is always the case; any number multiplied by 0 results in 0.
- Second Multiple (6 x 1): 6 multiplied by 1 equals 6. Multiplying any number by 1 always results in the original number itself.
- Third Multiple (6 x 2): 6 multiplied by 2 equals 12. This can be visualized as adding 6 to itself once (6 + 6 = 12).
- Fourth Multiple (6 x 3): 6 multiplied by 3 equals 18. This can be visualized as adding 6 to itself twice (6 + 6 + 6 = 18).
Therefore, the first four multiples of 6 are 0, 6, 12, and 18.
Beyond Simple Calculation: Understanding the Pattern
While calculating these multiples is straightforward, it's crucial to understand the underlying pattern. Notice that each subsequent multiple is obtained by adding 6 to the previous multiple. This constant difference highlights the consistent relationship between consecutive multiples of any given number. This pattern is essential for predicting future multiples and understanding the structure of number sequences.
This consistent addition of 6 also forms an arithmetic sequence. Arithmetic sequences are characterized by a constant difference between consecutive terms. Understanding arithmetic sequences is a crucial stepping stone to more advanced mathematical concepts, such as linear equations and functions.
Visualizing Multiples: A Graphical Representation
Visualizing mathematical concepts often aids understanding. We can represent the multiples of 6 graphically using a number line or a bar chart.
A number line would show the multiples of 6 as evenly spaced points along a line, emphasizing the consistent increment of 6 between each multiple. A bar chart could represent each multiple with a bar of corresponding height, providing a visual comparison of their values. Such visualizations reinforce the concept of consistent addition and the sequential nature of multiples.
Real-World Applications: Multiples in Everyday Life
The concept of multiples isn't confined to the classroom; it permeates our daily lives in numerous ways. Here are a few examples:
- Counting objects: If you have boxes containing 6 items each, the total number of items will always be a multiple of 6 (e.g., 6 boxes = 36 items, 10 boxes = 60 items).
- Time measurement: There are 60 minutes in an hour and 60 seconds in a minute. Calculations involving time frequently involve multiples of 60.
- Geometry and Measurement: Calculating perimeters or areas of shapes often involves multiples, especially when dealing with regular polygons or objects with symmetrical dimensions.
- Retail and Finance: Discounts, sales, and interest calculations often involve multiples of specific amounts.
Exploring Divisibility: The Inverse Relationship
The concept of multiples is closely linked to the concept of divisibility. A number is divisible by another number if it is a multiple of that number. For instance, 18 is divisible by 6 because 18 is a multiple of 6 (6 x 3 = 18). This reciprocal relationship is crucial in simplifying fractions, finding common denominators, and solving various mathematical problems.
Advanced Concepts: LCM and GCD
Understanding multiples is foundational to comprehending more advanced concepts like the Least Common Multiple (LCM) and the Greatest Common Divisor (GCD).
- LCM: The LCM of two or more numbers is the smallest number that is a multiple of all the given numbers. For instance, finding the LCM is essential when adding or subtracting fractions with different denominators.
- GCD: The GCD of two or more numbers is the largest number that divides all the given numbers without leaving a remainder. The GCD is useful in simplifying fractions to their lowest terms.
Mastering multiples is a critical first step toward understanding and applying these more advanced concepts.
Different Methods of Calculating Multiples: Beyond Basic Multiplication
While simple multiplication is the most straightforward method, several other techniques can be used to find multiples, particularly useful for larger numbers or more complex scenarios.
- Repeated Addition: This is a more visual method, especially helpful for younger learners. To find the fourth multiple of 6, add 6 to itself three times (6 + 6 + 6 + 6 = 24). This reinforces the additive nature of multiplication.
- Skip Counting: Start at 0 and repeatedly add 6. This method is intuitive and strengthens number sense. Count: 0, 6, 12, 18, 24, and so on.
- Using a Multiplication Table: A multiplication table provides a quick and efficient way to find multiples of various numbers. Simply locate the row corresponding to 6 and read the products.
- Using a Calculator: For larger multiples, a calculator offers a convenient way to perform the multiplication.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a factor and a multiple?
A: A factor is a number that divides another number without leaving a remainder. A multiple is the result of multiplying a number by a whole number. For example, 2 and 3 are factors of 6, while 6, 12, and 18 are multiples of 6. They are inverse concepts.
Q2: Are there infinite multiples of 6?
A: Yes, there are infinitely many multiples of 6. Since you can multiply 6 by any whole number (and there are infinitely many whole numbers), there is no limit to the number of multiples.
Q3: How can I find the 10th multiple of 6?
A: Simply multiply 6 by 10: 6 x 10 = 60. The 10th multiple of 6 is 60.
Q4: What are some real-world examples where understanding multiples is important?
A: Many everyday tasks require understanding multiples, such as: dividing food evenly among people, calculating the cost of items bought in bulk, scheduling events that happen at regular intervals, and managing finances.
Q5: How can I help my child understand multiples better?
A: Use visual aids like counters or blocks to represent the multiplication process. Employ real-world examples relevant to their age group. Practice skip-counting and use multiplication tables. Make it engaging and fun!
Conclusion: The Importance of Mastering Multiples
Understanding the first four multiples of 6—0, 6, 12, and 18—is just the beginning. This exploration has moved beyond simple calculations to delve into the deeper mathematical principles involved. The concept of multiples is a fundamental building block in mathematics, underpinning numerous operations and applications. By mastering this concept, you pave the way for a stronger grasp of more complex mathematical ideas and develop problem-solving skills applicable across various fields. Remember that consistent practice and a visual, intuitive approach can make learning multiples—and mathematics in general—a rewarding and fulfilling experience. Keep exploring, keep asking questions, and you’ll unlock the fascinating world of numbers!
Latest Posts
Latest Posts
-
Find The Value Of A
Sep 23, 2025
-
M 2 In Cm 2
Sep 23, 2025
-
Difference Between Math And Arithmetic
Sep 23, 2025
-
Words That Begin With Ap
Sep 23, 2025
-
Convert 2 5 Into A Percentage
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about First Four Multiples Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.