Convert 2/5 Into A Percentage
seoindie
Sep 23, 2025 · 6 min read
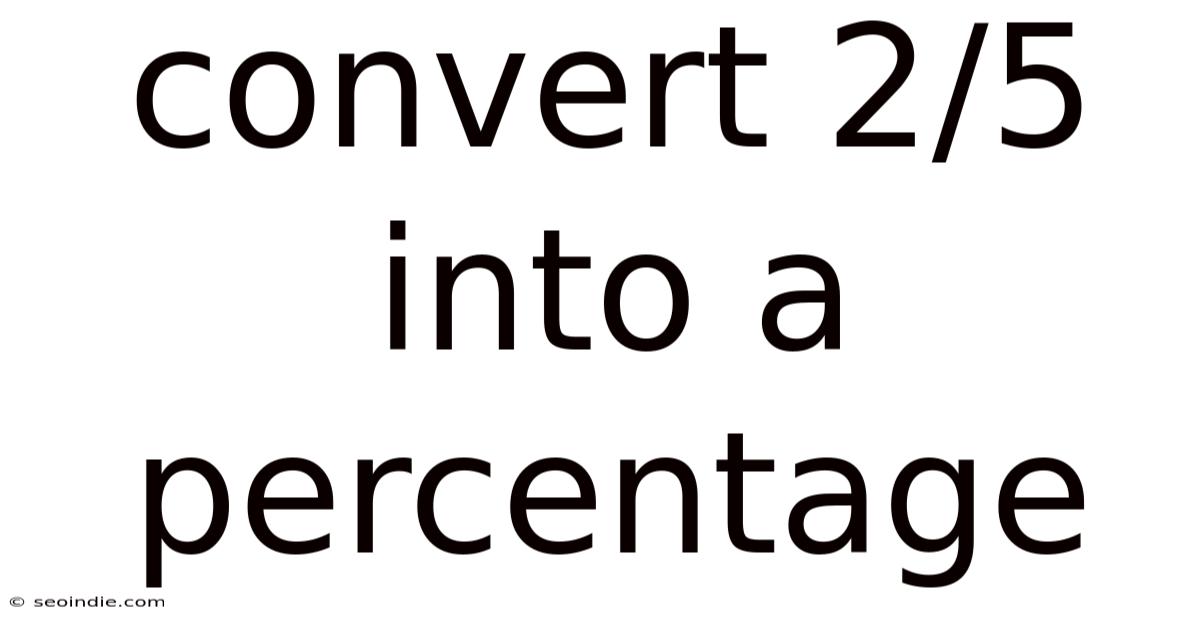
Table of Contents
Converting Fractions to Percentages: A Comprehensive Guide to Understanding 2/5 as a Percentage
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from everyday budgeting to advanced statistical analysis. This comprehensive guide will delve into the process of converting fractions to percentages, using the example of 2/5, while also exploring the underlying concepts and offering practical applications. We’ll uncover not just how to convert 2/5 into a percentage, but also why this process works and how you can apply it to countless other fractions.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 50% means 50 out of 100, which can also be written as the fraction 50/100.
Method 1: Converting 2/5 to a Percentage using the Decimal Equivalent
The most common method for converting a fraction to a percentage involves two steps: converting the fraction to a decimal and then converting the decimal to a percentage.
-
Convert the fraction to a decimal: To convert 2/5 to a decimal, we simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.4 × 100 = 40%
Therefore, 2/5 is equivalent to 40%.
Method 2: Converting 2/5 to a Percentage using Equivalent Fractions
Another approach involves creating an equivalent fraction with a denominator of 100. This method directly connects the fraction to the percentage definition.
-
Find an equivalent fraction with a denominator of 100: We need to find a number that, when multiplied by 5, gives us 100. This number is 20 (5 x 20 = 100).
-
Multiply both the numerator and denominator by the same number: To maintain the value of the fraction, we must multiply both the numerator and the denominator by 20:
(2 × 20) / (5 × 20) = 40/100
-
Express the fraction as a percentage: Since a percentage is a fraction out of 100, 40/100 is directly equivalent to 40%.
This method provides a clear visual representation of how the fraction relates to the percentage. It highlights the underlying principle that percentages are simply fractions expressed as parts of 100.
Method 3: Using Proportions to Convert 2/5 to a Percentage
This method utilizes the concept of proportions, offering a more algebraic approach to the conversion.
We can set up a proportion:
2/5 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
5x = 200
Then, divide both sides by 5:
x = 40
Therefore, 2/5 is equal to 40%. This method reinforces the relationship between fractions and percentages within a proportional framework.
Understanding the Concept: Why Does This Work?
The core principle behind these conversion methods is the fundamental relationship between fractions, decimals, and percentages. They are all different representations of the same value. A fraction expresses a part of a whole, a decimal expresses it as a portion of ten, hundredths, thousandths etc., and a percentage expresses it as a part of 100. By moving between these representations, we are simply changing the way we express the same numerical quantity.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in numerous real-world situations:
- Calculating discounts: If a store offers a 2/5 discount, converting this fraction (0.4 or 40%) allows for easy calculation of the final price.
- Determining grades: Many grading systems use percentages. Understanding how a fraction of correct answers translates to a percentage grade is essential.
- Analyzing data: In statistics and data analysis, representing data as percentages often makes it easier to understand and compare different proportions.
- Financial calculations: Interest rates, tax calculations, and profit margins are often expressed as percentages, requiring the conversion of fractions for accurate computations.
- Everyday life: From figuring out tips at restaurants to understanding sales tax, the ability to convert fractions to percentages is a practical skill applicable in daily life.
Beyond 2/5: Converting Other Fractions to Percentages
The methods described above can be applied to any fraction. The process remains the same: convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 to obtain the percentage.
For example:
- 3/4: 3 ÷ 4 = 0.75; 0.75 × 100 = 75%
- 1/8: 1 ÷ 8 = 0.125; 0.125 × 100 = 12.5%
- 7/10: 7 ÷ 10 = 0.7; 0.7 × 100 = 70%
Frequently Asked Questions (FAQ)
-
What if the fraction is an improper fraction (numerator larger than denominator)? The same methods apply. Convert the improper fraction to a mixed number or decimal, then convert the decimal to a percentage. For example, 7/5 = 1.4, and 1.4 x 100 = 140%.
-
What if the fraction has a very large denominator? Using a calculator makes the process easier. Divide the numerator by the denominator to get the decimal, and then multiply by 100 to find the percentage.
-
Can I convert percentages back to fractions? Absolutely! Divide the percentage by 100 and simplify the resulting fraction. For example, 60% becomes 60/100, which simplifies to 3/5.
-
Why is it important to learn this skill? Understanding fraction-to-percentage conversion enhances your mathematical proficiency, allowing you to solve problems efficiently and confidently in various academic and real-world scenarios.
Conclusion:
Converting 2/5 to a percentage—which equals 40%—is a straightforward process that relies on a fundamental understanding of fractions, decimals, and percentages. This guide has explored multiple methods for achieving this conversion, each offering a unique perspective on the underlying mathematical principles. By mastering this skill, you'll not only be able to solve specific problems but also gain a deeper understanding of how these mathematical concepts intertwine, making you more confident and proficient in numerical analysis. Remember, the key is to understand the why behind the how, and you’ll find that these seemingly simple conversions unlock a world of practical applications. Practice regularly, explore different fractions, and soon you'll be converting fractions to percentages with ease and accuracy.
Latest Posts
Latest Posts
-
Example Of An Inconsistent Equation
Sep 23, 2025
-
Hex To Decimal Conversion Table
Sep 23, 2025
-
The Vltage Valur At Which
Sep 23, 2025
-
First 20 Elements Electronic Configuration
Sep 23, 2025
-
Gcf Of 45 And 25
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Convert 2/5 Into A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.